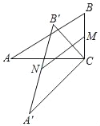
题目内容
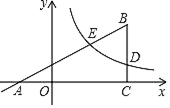
【题目】如图，△ABC中，M是AC的中点，E、F是BC上的两点，且BE=EF=FC.则BN:NQ:QM等于（ ）
A. 6:3:2 B. 2:1:1 C. 5:3:2 D. 1:1:1
【答案】C
【解析】
连结MF，如图，先证明MF为△CEA的中位线，则AE=2MF，AE∥MF，利用NE∥MF得到 
，
，即BN=NM，MF=2NF，设BN=a，NE=b，则NM=a，MF=2b，AE=4b，所以AN=3b，然后利用AN∥MF得到 
，所以NQ=
a，QM=
a，再计算BN：NQ：QM的值．
连结MF，如图，
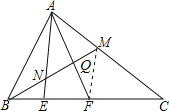
∵M是AC的中点，EF=FC，
∴MF为△CEA的中位线，
∴AE=2MF，AE∥MF，
∵NE∥MF，
∴，，
∴BN=NM，MF=2NF，
设BN=a，NE=b，则NM=a，MF=2b，AE=4b，
∴AN=3b，
∵AN∥MF，
∴，
∴NQ=a，QM=a，
∴BN：NQ：QM=a：a：a=5：3：2．
故选C．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某小区改善生态环境，实行生活垃圾的分类处理，将生活垃圾分成三类：厨房垃圾、可回收垃圾和其他垃圾，分别记为m，n，p，并且设置了相应的垃圾箱，“厨房垃圾”箱，“可回收垃圾”箱和“其他垃圾”箱，分别记为A，B，C.
(1)若将三类垃圾随机投入三类垃圾箱，请用画树状图的方法求垃圾投放正确的概率；
(2)为了了解居民生活垃圾分类投放的情况，现随机抽取了小区三类垃圾箱中总共1 000吨生活垃圾，数据统计如下(单位：吨)：
A | B | C | |
m | 400 | 100 | 100 |
n | 30 | 240 | 30 |
p | 20 | 20 | 60 |
请根据以上信息，试估计“厨房垃圾”投放正确的概率．
