题目内容
（2002•西藏）如果等边三角形的边长是3cm，那么它的一条高长为
．
3
| ||
| 2 |
3
| ||
| 2 |
分析：利用等边三角形的性质，构造直角三角形，然后利用勾股定理或三角函数求解．
解答：
解：如图，等边三角形△ABC，作高AD，则∠BAD=30°．
解法一：在Rt△ABD中，∵∠BAD=30°，
∴BD=
AB=
．
由勾股定理得：AD=
=
=
；
解法二：在Rt△ABD中，AD=AB•sin60°=3×
=
．
故答案为：
．
解：如图，等边三角形△ABC，作高AD，则∠BAD=30°．解法一：在Rt△ABD中，∵∠BAD=30°，
∴BD=
| 1 |
| 2 |
| 3 |
| 2 |
由勾股定理得：AD=
| AB2-BD2 |
32-(
|
3
| ||
| 2 |
解法二：在Rt△ABD中，AD=AB•sin60°=3×
| ||
| 2 |
3
| ||
| 2 |
故答案为：
3
| ||
| 2 |
点评：本题考查了等边三角形的基本性质，是基础题．
练习册系列答案
相关题目
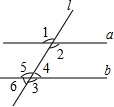（2002•西藏）如图，直线a∥直线b，直线l与a、b相交，那么下面的结论不能肯定正确的是（ ）
（2002•西藏）如图，△ABC中，∠C=90°，AB=2，sinB=0.4，那么AC的长是（ ）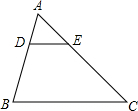
（2002•西藏）如图，D、E分别是△ABC中AB、AC边上的点，且AD：DB=AE：EC=1：2，那么△ADE与△ABC的面积之比是（ ）
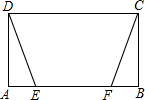（2002•西藏）已知：如图，矩形ABCD中，E、F是AB边上两点，且AF=BE，连结DE、CF得到梯形EFCD．
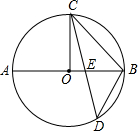（2002•西藏）已知，如图AB是⊙O的直径，半径OC⊥AB，弦CD与AB交于点E．