题目内容
(2011•临川区模拟)如图,已知正方形纸片ABCD,首先将正方形纸片对折,使AB与CD重合,折痕为EF,再沿直线CG折叠,使B点落在EF上,对应点为B′,连接A B′、D B′,则下列结论正确的是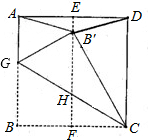 情给分)
情给分)
①EF平分线段GC;
②△GHB′是等边三角形;
③∠GAB′=75°;
④图中等腰三角形(等边三角形除外)共有4个.
①②③
①②③
.(多填或错填得0分,少填酌 情给分)
情给分)①EF平分线段GC;
②△GHB′是等边三角形;
③∠GAB′=75°;
④图中等腰三角形(等边三角形除外)共有4个.
分析:①根据正方形的性质可以得出四边相等和对边平行,再由轴对称的性质可以得出EF是BC的垂直平分线,最后根据平行线等分线段定理可以得出其结论.
②连接BB′,由对称轴的性质得出△BB′C为正三角形及△GB′C为直角三角形,从而得出∠BB′C=60°,得∠GB′B=∠GBB′=30°,由轴对称的性质得出BB′⊥GC,可以得出∠BGC=60°,从而证明△BB′C为等边三角形.
③由②得出∠GBB′=30°,且由轴对称得出△ABB′为等腰三角形,从而求出∠GAB′=75°.
④由①、②中的结论可以得出图中等腰三角形(含等边三角形)共有4个.
②连接BB′,由对称轴的性质得出△BB′C为正三角形及△GB′C为直角三角形,从而得出∠BB′C=60°,得∠GB′B=∠GBB′=30°,由轴对称的性质得出BB′⊥GC,可以得出∠BGC=60°,从而证明△BB′C为等边三角形.
③由②得出∠GBB′=30°,且由轴对称得出△ABB′为等腰三角形,从而求出∠GAB′=75°.
④由①、②中的结论可以得出图中等腰三角形(含等边三角形)共有4个.
解答: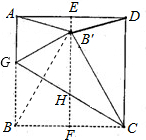 解:①∵四边形ABCD是正方形,
解:①∵四边形ABCD是正方形,
∴AB∥CD,AB=BC=CD=AD,
∵EF是对称轴,
∴AB∥EF∥CD,BF=CF,
∴
=
,
∴CH=GH,
∴EF平分线段GC;
故此结论正确;
②连接BB′.
∵GC是对称轴,
∴GC⊥BB′,BB′=B′C,BC=B′C,∠GB′C=90°,
∴△BB′C是正三角形,
∴∠BBC′=60°,
∴∠GB′B=∠GBB′=30°,
∴∠B′GC=60°.
∵CH=GH,
∴HB′=GH,
∴△GHB′是等边三角形.
故此结论正确;
③∵EF、GC是对称轴,
∴BB′=B′C,且B′C=AB,
∴BB′=AB且∠GBB′=30°,
∴∠GAB′=75°.
故此结论正确;
④在没有作辅助线的图中,由轴对称的性质和直角三角形的性质得出△AB′D、△B′DC、△HB′C、△HGB′是等腰三角形,但△HGB′是等边三角形.
故此结论错误.
故答案为:①②③.
 解:①∵四边形ABCD是正方形,
解:①∵四边形ABCD是正方形,∴AB∥CD,AB=BC=CD=AD,
∵EF是对称轴,
∴AB∥EF∥CD,BF=CF,
∴
| CH |
| GH |
| CF |
| BF |
∴CH=GH,
∴EF平分线段GC;
故此结论正确;
②连接BB′.
∵GC是对称轴,
∴GC⊥BB′,BB′=B′C,BC=B′C,∠GB′C=90°,
∴△BB′C是正三角形,
∴∠BBC′=60°,
∴∠GB′B=∠GBB′=30°,
∴∠B′GC=60°.
∵CH=GH,
∴HB′=GH,
∴△GHB′是等边三角形.
故此结论正确;
③∵EF、GC是对称轴,
∴BB′=B′C,且B′C=AB,
∴BB′=AB且∠GBB′=30°,
∴∠GAB′=75°.
故此结论正确;
④在没有作辅助线的图中,由轴对称的性质和直角三角形的性质得出△AB′D、△B′DC、△HB′C、△HGB′是等腰三角形,但△HGB′是等边三角形.
故此结论错误.
故答案为:①②③.
点评:本题是一道有关轴对称的试题,考查了轴对称的性质及运用,直角三角形的性质,等腰三角形的判定及运用,正方形的性质及平行线等分线段定理的运用.

练习册系列答案
相关题目
 (2011•临川区模拟)如图,梯形ABCD中,AB∥CD,AD=CD,E、F分别是AB,BC的中点,若∠D=108°,则∠1=
(2011•临川区模拟)如图,梯形ABCD中,AB∥CD,AD=CD,E、F分别是AB,BC的中点,若∠D=108°,则∠1=