题目内容
某市为创建省卫生城市,有关部门决定利用现有的4200盆甲种花卉和3090盆乙种花卉,搭配A、B两种园艺造型共60个,摆放于入城大道的两侧,搭配每个造型所需花卉数量的情况下表所示,结合上述信息,解答下列问题:
(1)符合题意的搭配方案有几种?
(2)如果搭配一个A种造型的成本为1000元,搭配一个B种造型的成本为1500元,试说明选用那种方案成本最低?最低成本为多少元?
(1)符合题意的搭配方案有几种?
(2)如果搭配一个A种造型的成本为1000元,搭配一个B种造型的成本为1500元,试说明选用那种方案成本最低?最低成本为多少元?
| 造型花卉 | 甲 | 乙 |
| A | 80 | 40 |
| B | 50 | 70 |
解:(1)设需要搭配x个A种造型,则需要搭配B种造型(60-x)个,
则有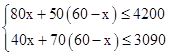 ,解得37≤x≤40,
,解得37≤x≤40,
∵x为正整数,∴x=37或38或39或40。
∴符合题意的搭配方案有4种:
第一方案:A种造型37个,B种造型23个;
第二种方案:A种造型38个,B种造型22个;
第三种方案:A种造型39个,B种造型21个.
第四种方案:A种造型40个,B种造型20个。
(2)设A、B两种园艺造型分别为x,(50-x)个时的成本为z元,
则: 。
。
∵-500<0,∴成本z随着x的增大而减小。
∴当x=40时,成本最低。最低成本为70000。
答:选择第四种方案成本最低,最低位70000元。
则有
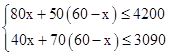 ,解得37≤x≤40,
,解得37≤x≤40,∵x为正整数,∴x=37或38或39或40。
∴符合题意的搭配方案有4种:
第一方案:A种造型37个,B种造型23个;
第二种方案:A种造型38个,B种造型22个;
第三种方案:A种造型39个,B种造型21个.
第四种方案:A种造型40个,B种造型20个。
(2)设A、B两种园艺造型分别为x,(50-x)个时的成本为z元,
则:
 。
。∵-500<0,∴成本z随着x的增大而减小。
∴当x=40时,成本最低。最低成本为70000。
答:选择第四种方案成本最低,最低位70000元。
一元一次不等式组和一次函数的应用。
【分析】(1)设需要搭配x个A种造型,则需要搭配B种造型(60-x)个,根据“4200盆甲种花卉”“3090盆乙种花卉”列不等式求解,取整数值即可。
(2)列出成本z关于A种造型个数x的函数关系式,根据一次函数的增减性求出答案。
【分析】(1)设需要搭配x个A种造型,则需要搭配B种造型(60-x)个,根据“4200盆甲种花卉”“3090盆乙种花卉”列不等式求解,取整数值即可。
(2)列出成本z关于A种造型个数x的函数关系式,根据一次函数的增减性求出答案。

练习册系列答案
相关题目
 与
与 轴负半轴、
轴负半轴、 轴正半轴分别交于A、B两点,正比例函数
轴正半轴分别交于A、B两点,正比例函数 的图像与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM =10,BN =3,
的图像与直线AB交于点Q,过A、B两点分别作AM⊥OQ于M,BN⊥OQ于N,若AM =10,BN =3,

 中,AB∥CD;
中,AB∥CD; ⊥
⊥ 动点
动点 从点
从点 出发,沿
出发,沿 停止.设点
停止.设点 ,
, 的面积为
的面积为 ,如果
,如果 的面积是( )
的面积是( )
 垄,通过计算说明共有几种种植方案?分别是哪几种?
垄,通过计算说明共有几种种植方案?分别是哪几种? 的图象如右图所示,则不等式
的图象如右图所示,则不等式 的解集为 .
的解集为 .
 (
( ,
, 为常数)的图象如图,化简:︱
为常数)的图象如图,化简:︱ ︱-
︱- 得
得 
 B.5 C.-1 D.
B.5 C.-1 D.
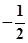 对称,则t的值为( )
对称,则t的值为( ) (2, 4)在函数
(2, 4)在函数 的图象上,则下列各点也在此函数图象上的是
的图象上,则下列各点也在此函数图象上的是