题目内容
【题目】在平面直角坐标系![]() 中,对于任意三点
中,对于任意三点![]() ,
,![]() ,
,![]() 给出如下定义:如果矩形的任何一条边均与某条坐标轴平行或共线,且
给出如下定义:如果矩形的任何一条边均与某条坐标轴平行或共线,且![]() ,
,![]() ,
,![]() 三点都在矩形的内部或边界上,那么称该矩形为点
三点都在矩形的内部或边界上,那么称该矩形为点![]() ,
,![]() ,
,![]() 的外延矩形,在点
的外延矩形,在点![]() ,
,![]() ,
,![]() 所有的外延矩形中,面积最小的矩形称为点
所有的外延矩形中,面积最小的矩形称为点![]() ,
,![]() ,
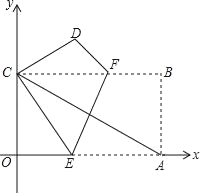
,![]() 的最佳外延矩形.例如,图
的最佳外延矩形.例如,图![]() 中的矩形
中的矩形![]() ,
,![]() ,
,![]() 都是点
都是点![]() ,
,![]() ,
,![]() 的外延矩形,矩形
的外延矩形,矩形![]() 是点
是点![]() ,
,![]() ,
,![]() 的最佳外延矩形.
的最佳外延矩形.



(![]() )如图
)如图![]() ,点
,点![]() ,
,![]() ,
,![]() (
(![]() 为整数).
为整数).
①如果![]() ,则点
,则点![]() ,
,![]() ,
,![]() 的最佳外延矩形的面积是__________.
的最佳外延矩形的面积是__________.
②如果点![]() ,
,![]() ,
,![]() 的最佳外延矩形的面积是
的最佳外延矩形的面积是![]() ,且使点
,且使点![]() 在最佳外延矩形的一边上,请写出一个符合题意的
在最佳外延矩形的一边上,请写出一个符合题意的![]() 值__________.
值__________.
(![]() )如图
)如图![]() ,已知点
,已知点![]() 在函数
在函数![]() 的图象上,且点
的图象上,且点![]() 的坐标为
的坐标为![]() ,求点
,求点![]() ,
,![]() ,
,![]() 的最佳外延矩形的面积
的最佳外延矩形的面积![]() 的取值范围以及该面积最小时
的取值范围以及该面积最小时![]() 的取值范围.
的取值范围.
【答案】(![]() )①
)①![]() .②
.②![]() 或
或![]() .(
.(![]() )
)![]() ,
,![]()
【解析】试题分析:(1)①根据所给的最佳外延矩形的定义求解即可;②由点A(-1,0),B(2,4),可得AB=3,又因最佳外延矩形面积为![]() ,可得最佳外延矩形的另一边长为8,即
,可得最佳外延矩形的另一边长为8,即![]() 或
或![]() ,由此即可求得
,由此即可求得![]() 或
或![]() ;(2)当
;(2)当![]() 时,
时,![]() ,即
,即![]() ,此时
,此时![]() ,当
,当![]() 时,
时,![]() ,即
,即![]() ,此时
,此时![]() .所以当
.所以当![]() 时,
时,![]() ,当
,当![]() 在其它处位置时,
在其它处位置时,![]() ,由此即可求得结论.
,由此即可求得结论.
试题解析:
(![]() )①当
)①当![]() 时,
时,
最佳外延矩形的面积为![]() .
.
②由最佳外延矩形面积为![]() ,得
,得![]() ,
,
即![]() ,
,
∴![]() ,
,
又∵![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
∴![]() 或
或![]() ,
,
即![]() 或
或![]() .
.
(![]() )当
)当![]() 时,
时,![]() ,即
,即![]() ,
,
此时![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
此时![]() .
.
∴当![]() 时,
时,![]() ,
,
当![]() 在其它处位置时,
在其它处位置时,![]() ,
,
∴综上![]() ,当
,当![]() 时,
时,![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目