题目内容
【题目】如图所示,把矩形纸片OABC放入直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,连接AC,且AC=4![]() ,
, ![]()
(1)求AC所在直线的解析式;
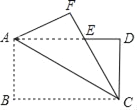
(2)将纸片OABC折叠,使点A与点C重合(折痕为EF),求折叠后纸片重叠部分的面积.
(3)求EF所在的直线的函数解析式.

【答案】(1)y=﹣![]() x+4;(2)重叠部分的面积为10;(3)y=2x﹣6
x+4;(2)重叠部分的面积为10;(3)y=2x﹣6
【解析】试题分析:
(1)设OC=x,则OA=2x,在Rt△AOC中,由勾股定理建立方程,解方程求得x的值,即可得到点A、C的坐标,根据所得A、C两点的坐标用待定系数法求出直线AC的解析式即可;
(2)由折叠的性质可得AE=CE,设AE=CE=y,结合OA=8,可得OE=8-y,在Rt△OCE中由勾股定理建立方程解方程求得y的值即可得到CE的值,再证∠CEF=∠AEF=∠CFE可得CF=CE,这样即可由三角形面积公式求出△CEF的面积了.
(3)由(2)可知OE,CF的长,从而可得点E、F的坐标,由此即可用待定系数法求得直线EF的解析式了.
试题解析:
(1)∵![]() ,
,
∴ 可设OC=x,则OA=2x,
在Rt△AOC中,由勾股定理可得OC2+OA2=AC2,
∴x2+(2x)2=(4![]() )2,解得x=4或x=﹣4(不合题意,舍去),
)2,解得x=4或x=﹣4(不合题意,舍去),
∴OC=4,OA=8,
∴A(8,0),C(0,4),
设直线AC解析式为y=kx+b,
∴![]() ,解得:
,解得: 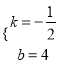 ,
,
∴直线AC解析式为y=![]() x+4;
x+4;
(2)由折叠的性质可知AE=CE,
设AE=CE=y,则OE=8﹣y,
在Rt△OCE中,由勾股定理可得OE2+OC2=CE2,
∴(8﹣y)2+42=y2,解得y=5,
∴AE=CE=5,
∵∠AEF=∠CEF,∠CFE=∠AEF,
∴∠CFE=∠CEF,
∴CE=CF=5,
∴S△CEF=![]() CFOC=
CFOC=![]() ×5×4=10,
×5×4=10,
即重叠部分的面积为10;
(3)由(2)可知OE=3,CF=5,
∴E(3,0),F(5,4),
设直线EF的解析式为y=k′x+b′,
∴![]() ,解得:
,解得: ![]() ,
,
∴直线EF的解析式为y=2x﹣6.

 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案