题目内容
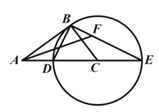
【题目】如图,在Rt△ABC中,∠ABC=90°,以CB为半径作⊙C,交AC于点D,交AC的延长线于点E,连接ED,BE.(1)求证:△ABD∽△AEB;(2)当![]() 时,求tanE;
时,求tanE;
【答案】(1)证明见解析;(2) ![]() .
.
【解析】(1)要证明△ABD∽△AEB,已经有一组对应角是公共角,只需要再找出另一组对应角相等即可.
(2)由于AB:BC=4:3,可设AB=4,BC=3,求出AC的值,再利用(1)中结论可得AB2=ADAE,进而求出AE的值,所以tanE=![]() .
.
解:(1)∵∠ABC=90°,
∴∠ABD=90°﹣∠DBC,
由题意知:DE是直径,
∴∠DBE=90°,
∴∠E=90°﹣∠BDE,
∵BC=CD,
∴∠DBC=∠BDE,
∴∠ABD=∠E,
∵∠A=∠A,
∴△ABD∽△AEB;
(2)∵AB:BC=4:3,
∴设AB=4,BC=3,
∴AC=![]() =5,
=5,
∵BC=CD=3,
∴AD=AC﹣CD=5﹣3=2,
由(1)可知:△ABD∽△AEB,
∴![]() ,
,
∴AB2=ADAE,
∴42=2AE,
∴AE=8,
在Rt△DBE中
tanE=![]() .
.
“点睛“此题属于圆的综合题,涉及了相似三角形判定与性质、三角函数值的知识,综合性较强,解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目



