题目内容
【题目】(1)、如图（1），AB∥CD，点P在AB、CD外部，若∠B=40°，∠D=15°，则∠BPD °．
(2)、如图（2），AB∥CD，点P在AB、CD内部，则∠B，∠BPD，∠D之间有何数量关系？证明你的结论；
(3)、在图（2）中，将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点M，如图（3），若∠BPD=90°，∠BMD=40°，求∠B+∠D的度数．
【答案】(1)、25°；(2)、∠BPD=∠B+∠D，理由见解析；(3)、50°.
【解析】
试题分析：(1)、根据AB∥CD得出∠BOD=∠B=40°，然后根据三角形外角的性质得出∠BPD的度数；(2)、过点P作PE∥AB，从而得出AB∥PE∥CD，根据平行线的性质得出∠1=∠B，∠2=∠D，最后根据∠BPD=∠1+∠2得出答案；(3)、过点P作GP∥AB交CD于E，过点P作PF∥CD，根据平行线的性质得出∠BMD=∠GED=∠GPF=50°，∠B=∠BPG，∠D=∠DPF，则∠B+∠D=∠BPG+∠DPF，从而得出答案.
试题解析：(1)、∵AB∥CD（已知） ∴∠BOD=∠B=40°（两直线平行，内错角相等）
∴∠P=∠BOD﹣∠D=40°﹣15°=25°（等式的性质）
(2)、∠BPD=∠B+∠D．理由如下：
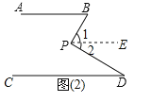
过点P作PE∥AB ∵AB∥CD，PE∥AB（已知） ∴AB∥PE∥CD（平行于同一直线的两条直线平行）
∴∠1=∠B，∠2=∠D（两直线平行，内错角相等） ∴∠BPD=∠1+∠2=∠B+∠D（等量代换）
(3)、过点P作GP∥AB交CD于E 过点P作PF∥CD
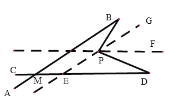
∵ PE∥AB
∴∠BMD=∠GED=∠GPF=50° ∠B=∠BPG（两直线平行，内错角相等）
∵ PF∥CD ∴∠D=∠DPF（两直线平行，内错角相等） ∴∠B+∠D=∠BPG+∠DPF（等量代换）
即∠B+∠D =∠BPD－∠GPF=∠BPD－∠BMD=90°- 40°=50°
教材全解字词句篇系列答案
【题目】永州市是一个降水丰富的地区，今年4月初，某地连续降雨导致该地某水库水位持续上涨，下表是该水库4月1日~4月4日的水位变化情况：
日期x | 1 | 2 | 3 | 4 |
水位y(米) | 20．00 | 20．50 | 21．00 | 21．50 |
(1)请建立该水库水位y与日期x之间的函数模型；
(2)请用求出的函数表达式预测该水库今年4月6日的水位；
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗？
