题目内容
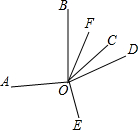 如图,从点O引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,则∠COD的度数为
如图,从点O引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,则∠COD的度数为20°
20°
.分析:设∠COD=x,∠BOC+∠AOD=y,由OF平分∠BOC,∠AOE=∠DOE,可得x+
y=140°,图中六个角之和为360°,可得x+y+100°=360°,联立方程组解得x.
| 1 |
| 2 |
解答:解:设∠COD=x,∠BOC+∠AOD=y,
∵OF平分∠BOC,∠AOE=∠DOE=
∠BOC,
∵∠EOF=140°,∠AOB=100°
∴x+
y=140° ①,
∵六个角之和为360°,
∴x+y+100°=360° ②,
联立①②解得:x=20°,
∴∠COD的度数为20°.
故答案为:20°.
∵OF平分∠BOC,∠AOE=∠DOE=
| 1 |
| 2 |
∵∠EOF=140°,∠AOB=100°
∴x+
| 1 |
| 2 |
∵六个角之和为360°,
∴x+y+100°=360° ②,
联立①②解得:x=20°,
∴∠COD的度数为20°.
故答案为:20°.
点评:本题考查角与角之间的运算,注意结合图形,发现角与角之间的关系,进而求解.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
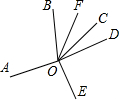 如图,从点O引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,求∠COD的度数.
如图,从点O引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,求∠COD的度数. 如图,从点O引出4条射线,OC平分∠BOD,则:
如图,从点O引出4条射线,OC平分∠BOD,则: 如图,从点O引出4条射线,OC平分∠BOD,则:
如图,从点O引出4条射线,OC平分∠BOD,则: ∠BOD=______;
∠BOD=______; 如图,从点O引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,求∠COD的度数.
如图,从点O引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,求∠COD的度数.