题目内容
 如图,从点O引出4条射线,OC平分∠BOD,则:
如图,从点O引出4条射线,OC平分∠BOD,则:
(1)∠AOC+ ∠BOD=______;
∠BOD=______;
(2)∠AOD-2∠BOC=______;
(3)∠AOC+∠BOD=______+∠AOD.
解:(1)∵OC平分∠BOD,
∴∠COD= ∠BOD,
∠BOD,
∴∠AOC+ ∠BOD=∠AOC+∠COD=∠AOD;
∠BOD=∠AOC+∠COD=∠AOD;
(2)∵OC平分∠BOD,
∴∠BOD=2∠BOC,
∴∠AOD-2∠BOC=∠AOD-∠BOD=∠AOB;
(3)∵∠AOC+∠BOD=∠AOC+∠BOC+∠COD=∠BOC+∠AOD.
故答案为∠AOD;∠AOB;∠BOC.
分析:(1)根据角平分线的定义得到∠COD= ∠BOD,则∠AOC+
∠BOD,则∠AOC+ ∠BOD=∠AOC+∠COD=∠AOD;
∠BOD=∠AOC+∠COD=∠AOD;
(2)根据角平分线的定义得到∠BOD=2∠BOC,则∠AOD-2∠BOC=∠AOD-∠BOD=∠AOB;
(3)利用∠AOC+∠BOD=∠AOC+∠BOC+∠COD=∠BOC+∠AOD得到答案.
点评:本题考查了角平分线的定义:从一个角的顶点出发的一条射线把角分成相等的两部分,这条射线叫这个角的平分线.
∴∠COD=
 ∠BOD,
∠BOD,∴∠AOC+
 ∠BOD=∠AOC+∠COD=∠AOD;
∠BOD=∠AOC+∠COD=∠AOD;(2)∵OC平分∠BOD,
∴∠BOD=2∠BOC,
∴∠AOD-2∠BOC=∠AOD-∠BOD=∠AOB;
(3)∵∠AOC+∠BOD=∠AOC+∠BOC+∠COD=∠BOC+∠AOD.
故答案为∠AOD;∠AOB;∠BOC.
分析:(1)根据角平分线的定义得到∠COD=
 ∠BOD,则∠AOC+
∠BOD,则∠AOC+ ∠BOD=∠AOC+∠COD=∠AOD;
∠BOD=∠AOC+∠COD=∠AOD;(2)根据角平分线的定义得到∠BOD=2∠BOC,则∠AOD-2∠BOC=∠AOD-∠BOD=∠AOB;
(3)利用∠AOC+∠BOD=∠AOC+∠BOC+∠COD=∠BOC+∠AOD得到答案.
点评:本题考查了角平分线的定义:从一个角的顶点出发的一条射线把角分成相等的两部分,这条射线叫这个角的平分线.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
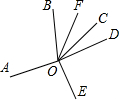 如图,从点O引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,求∠COD的度数.
如图,从点O引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,求∠COD的度数.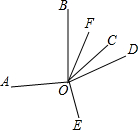 如图,从点O引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,则∠COD的度数为
如图,从点O引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,则∠COD的度数为 如图,从点O引出4条射线,OC平分∠BOD,则:
如图,从点O引出4条射线,OC平分∠BOD,则: 如图,从点O引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,求∠COD的度数.
如图,从点O引出6条射线OA、OB、OC、OD、OE、OF,且∠AOB=100°,OF平分∠BOC,∠AOE=∠DOE,∠EOF=140°,求∠COD的度数.