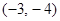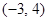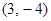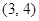题目内容
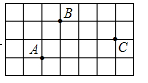
如图,在平面直角坐标系中有一边长为l的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1,再以对角线OBl为边作第三个正方形OBlB2C2,照此规律作下去,则点B2012的坐标为 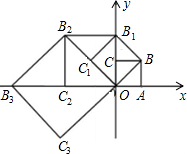

(-21006,-21006)。
分OBi的长度和点Bi的位置分别寻找规律:
由正方形边长为1,根据勾股定理可得
OB=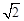 ,OB1=2=
,OB1=2=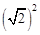 ,OB2=2
,OB2=2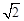 =
=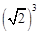 ,
,
OB3=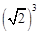 ·
·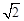 =
= ,……OB2012=
,……OB2012=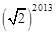 。
。
如图,点Bi的位置为i=8一个周期。
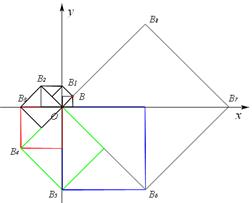
∵2012÷8=251……4,
∴点B2012的坐标与点B4的坐标位置相同,都在第三象限。
由正方形的性质可知△OB2011B2012是等腰直角三角形。
∴B2011B2012="O" B2011=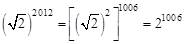 。
。
∴点B2012的坐标为(-21006,-21006)。
由正方形边长为1,根据勾股定理可得
OB=
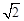 ,OB1=2=
,OB1=2=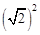 ,OB2=2
,OB2=2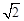 =
=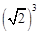 ,
,OB3=
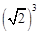 ·
·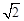 =
= ,……OB2012=
,……OB2012=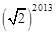 。
。如图,点Bi的位置为i=8一个周期。

∵2012÷8=251……4,
∴点B2012的坐标与点B4的坐标位置相同,都在第三象限。
由正方形的性质可知△OB2011B2012是等腰直角三角形。
∴B2011B2012="O" B2011=
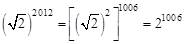 。
。∴点B2012的坐标为(-21006,-21006)。

练习册系列答案
相关题目
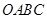 沿
沿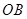 对折,使点
对折,使点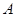 落在点
落在点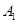 处,已知
处,已知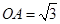 ,
,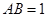 ,则点
,则点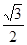 ,
, )
) ,
,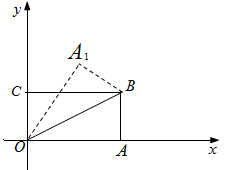
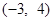 与点
与点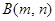 关于
关于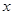 轴对称,则点
轴对称,则点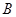 的坐标为( )
的坐标为( )