题目内容
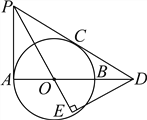
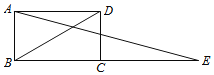
【题目】如图，延长矩形ABCD的边BC至点E，使CE＝BD，连结AE，如果∠ABD＝m°，则∠E＝_____度（用含m的代数式表示）．
【答案】45－
m
【解析】
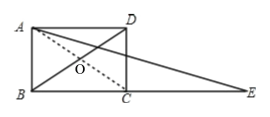
连接AC，由矩形性质可得∠ABC=90°，AC=BD，OB=OC，继而可得∠OCB=∠OBC，∠E=∠CAE，由∠ABD=m°，可得∠OBC=90°-m°，再由三角形外角的性质即可求得答案.
连接AC，交BD于点O，
∵四边形ABCD是矩形，
∴∠ABC=90°，AC=BD，OB=OC，
∴∠OCB=∠OBC，
又∵BD=CE，
∴CE=CA，
∴∠E=∠CAE，
∵∠ABD=m°，
∴∠OBC=∠ABC-∠ABD=90°-m°，
∵∠OCB=∠CAE+∠E，
∴∠E+∠E=90°-m°，
∴∠E=(45－m)°，
故答案为：45－m．
练习册系列答案
相关题目
【题目】某校数学兴趣小组成员小华对本班上学期期末考试数学成绩（成绩取整数，满分为100分）作了统计分析，绘制成如下频数分布直方图和频数、频率分布表．请你根据图表提供的信息，解答下列问题：
分组 | 49.5～59.5 | 59.5～69.5 | 69.5～79.5 | 79.5～89.5 | 89.5～100.5 | 合计 |
频数 | 2 |
| 20 | 16 | 4 | 50 |
频率 | 0.04 | 0.16 | 0.40 | 0.32 |
| 1 |
（1）频数、频率分布表中
，
；
（2）补全频数分布直方图；
（3）数学老师准备从不低于90分的学生中选1人介绍学习经验，那么取得了93分的小华被选上的概率是多少？
【题目】2018年12月4日是第五个国家宪法日，也是第一个“宪法宣传周”．甲、乙两班各选派10名学生参加宪法知识竞赛（满分100分），成绩如下：
成绩 | 85 | 90 | 95 | 100 |
甲班参赛学生/人 | 1 | 1 | 5 | 3 |
乙班参赛学生/人 | 1 | 2 | 3 | 4 |
分别求甲、乙两班参赛学生竞赛成绩的平均数和方差．
