题目内容
如图所示,已知圆锥底面半径r=10cm,母线长为40cm.
小题1:求它的侧面展开图的圆心角和表面积.
小题2:若一甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是多少?为什么?
小题1:求它的侧面展开图的圆心角和表面积.
小题2:若一甲虫从A点出发沿着圆锥侧面行到母线SA的中点B,请你动脑筋想一想它所走的最短路线是多少?为什么?

小题1:)90° 500
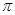
小题2:如图,这是一道开放题,由圆锥的侧面展开图可见,甲虫从A点出发沿着圆锥侧面绕行到母线SA的中点B所走的最短路线是线段AB的长,在Rt△ASB中,SA=40,SB=20,∴AB=20
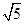 (cm),∴甲虫走的最短路线的长度是20
(cm),∴甲虫走的最短路线的长度是20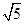 cm.
cm.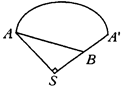
(1)利用圆锥的弧长等于底面周长得到圆锥的侧面展开图的圆心角;圆锥表面积=底面积+侧面积=π×底面半径2+π×底面半径×母线长;
(2)最短路线应放在平面内,构造直角三角形,求两点之间的线段的长度.
解:(1)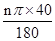 =2π×10,
=2π×10,
解得n=90°.
圆锥表面积=π×102+π×10×40=500πcm2.
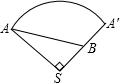
(2)如右图,由圆锥的侧面展开图可见,甲虫从A点出发沿着圆锥侧面绕行到母线SA的中点B所走的最短路线是线段AB的长.
在Rt△ASB中,SA=40,SB=20,
∴AB=20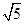 (cm).
(cm).
∴甲虫走的最短路线的长度是20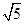 cm.
cm.
(2)最短路线应放在平面内,构造直角三角形,求两点之间的线段的长度.
解:(1)
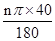 =2π×10,
=2π×10,
解得n=90°.
圆锥表面积=π×102+π×10×40=500πcm2.
(2)如右图,由圆锥的侧面展开图可见,甲虫从A点出发沿着圆锥侧面绕行到母线SA的中点B所走的最短路线是线段AB的长.
在Rt△ASB中,SA=40,SB=20,
∴AB=20
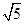 (cm).
(cm).∴甲虫走的最短路线的长度是20
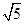 cm.
cm.
练习册系列答案
相关题目
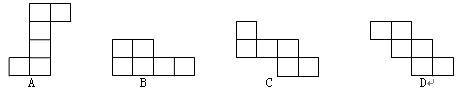
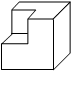
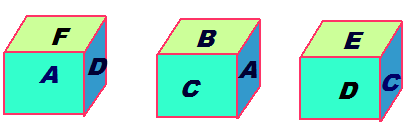
 的正方体的表面(不考虑接缝),如图2所示.小明所用正方形包装纸的边长至少为 ________________
的正方体的表面(不考虑接缝),如图2所示.小明所用正方形包装纸的边长至少为 ________________



 已知直四棱柱的底面是边长为a的正方形, 高为
已知直四棱柱的底面是边长为a的正方形, 高为 , 体积为V, 表面积等于S. 当a =" 2," h =
, 体积为V, 表面积等于S. 当a =" 2," h = 时,分别求V和S.
时,分别求V和S.