题目内容
【题目】如图,将边长为4的正方形OABC置于平面直角坐标系中,点P在边OA上从O向A运动,连接CP交对角线OB于点Q,连接AQ. 
(1)求证:△OCQ≌△OAQ;
(2)当点Q的坐标为( ![]() ,
, ![]() )时,求点P的坐标;
)时,求点P的坐标;
(3)若点P在边OA上从点O运动到点A后,再继续在边AB上从A运动到点B,在整个过运动过程中,若△OCQ恰为等腰三角形,请直接写出所有满足条件的点P的坐标. 
【答案】
(1)证明:∵四边形OCBA是正方形,
∴OC=OA,∠COD=∠AOD=45°,
在△OCD和△OAD中 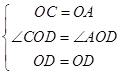 ,
,
∴△OCD≌△OAD(SAS),
(2)解:∵点Q的坐标为( ![]() ,
, ![]() ),
),
∴OQ= ![]() ,
,
在正方形OABC中,BC∥OA,OC=BC=4,
∴OB=4 ![]() ,
,
∴BQ=OB﹣OQ= ![]() ,
,
∵BC∥OA,
∴△OQP∽△BQC,
∴ ![]() ,
,
∴ 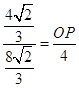 ,
,
∴OP=2,
∴P(2,0);
(3)解:解:分为三种情况:
①OC=OD时,如图1,
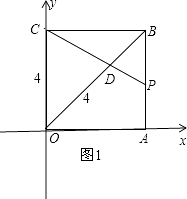
∴OD=4,
∵OB=4 ![]() ,
,
∴BD=OB﹣OD=4 ![]() ﹣4,
﹣4,
∵∠BOC=45°,
∴∠OCP=67.5°,
∴点P在AB上,
∵OC∥AB,
∴△ODC∽△BDP,
∴ ![]() ,
,
∴ ![]() ,
,
∴BP=4 ![]() ﹣4,
﹣4,
∴AP=AB﹣BP=4﹣(4 ![]() ﹣4)=8﹣4
﹣4)=8﹣4 ![]() ,
,
∴P点的坐标是(4,8﹣4 ![]() );
);
②CD=OD时,如图2,
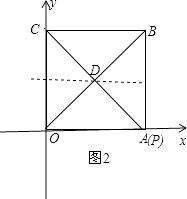
∵∠BOC=45°,
∴点D是OB的中点,
∴点P与点A重合,
∴P点的坐标是(4,0);
③OC=CD时,
∴∠CDO=∠COD=45°.
∴∠OCD=90°,
∴点P和点B重合,
∴P点的坐标是(4,4).
即满足条件的点P的坐标为(4,8﹣4 ![]() )或(4,0)或(4,4).
)或(4,0)或(4,4).
【解析】(1)根据正方形性质推出OC=OA,∠COD=∠AOD=45°,根据SAS证明三角形全等即可;(2)先求出OB,OQ,进而判断出△OQP∽△BQC,即可得出结论.(3)分为三种情况:①OC=OD时,②CD=OD时,③OC=CD时,根据等腰三角形性质和相似求出即可.
【考点精析】本题主要考查了等腰三角形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.