��Ŀ����
����Ŀ��A��B��C��D��E��F������ӽ��е�ѭ��������ÿ����֮����һ���������������ֳ�ʤ������ÿ��ͬʱ���������ظ�����һ��������ǰ����Ļ��ֱ����£�E��F�Ļ��ֱ��ڵ�����
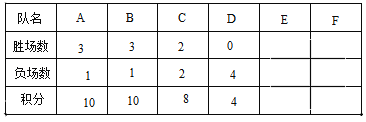
��1�����ݻ��ְ�ʤһ�������֣���һ�������֣�
��2����E��ǰ������ֱ�F�Ӷ�4�֣���E��F����ǰ�����ս���ֱ��Ǽ�ʤ������
��3����֪��һ��B��D���ڶ���C��E��������D��F��������B��C�����Է���������A��˭���������
���𰸡���1��ʤһ����3�֣���һ����1�֣���2��E��3ʤ1����F��1ʤ3������3��������A��B���������
��������
��1����D�ӿ�֪��һ����1�֣���ʤһ����x�֣����ܸ��ݱ��������ӵ÷�����з�����x��ֵ��
��2���ֱ���E��F��ʤy����z������4��y�����ͣ�4��z����������E�Ի��ֱ�F�Զ�4�ֿ��е�һ�����̣���ǰ���칲�����3��4��12���������ж���ʤ�ij���Ϊ12�����еõڶ������̣����������鼴����y��z��ֵ��
��3���������漰B�ı����϶࣬�ɴ�B�����֣��ڶ���B��������C�����������D����һ�����E�����������б���������ֻ����A��F�������÷�֤��������ڶ���B��A��������������Ϊ��A��B��C��E��D��F����D��F�ǵ�����Ŷ��ʳ���ì�ܣ����ڶ���B����A�������F��������BҪ�ڵ�������A���ô𰸣�
�⣺��1����D������ɵã���4����4��
�ฺһ����1��
��ʤһ����x�֣��ã�3x+1��10
��ã�x��3
��ʤһ����3�֣���һ����1�֣�
��2����E��ʤy����F��ʤz����������ã�
![]() ��ã�
��ã�![]() ��
��
��E��3ʤ1����F��1ʤ3����
��3����������֪���ڶ���B��A��F����
���ڶ���B��A������������ǣ�B��A��C��E��D��F������������D��F����ì�ܣ���������
��ڶ���B��F������Ϊ��C��E��B��F��A��D
�������B��A����
�𣺵�����A��B���������