题目内容
对于任意的两个实数对(a,b)和(c,d),规定:
①(a,b)=(c,d),当且仅当a=c,b=d;
②运算“?”为:(a,b)?(c,d)=(ac+bd,bc-ad);
③运算“θ”为:(a,b)θ(c,d)=(a-c,b-d).
设p,q∈R,若(1,2)?(p,q)=(11,2),则(1,2)θ(p,q)( )
①(a,b)=(c,d),当且仅当a=c,b=d;
②运算“?”为:(a,b)?(c,d)=(ac+bd,bc-ad);
③运算“θ”为:(a,b)θ(c,d)=(a-c,b-d).
设p,q∈R,若(1,2)?(p,q)=(11,2),则(1,2)θ(p,q)( )
分析:先根据(1,2)?(p,q)=(11,2),列方程组求p、q的值,再由规定运算“θ”求(1,2)θ(p,q)的结果.
解答:解:由规定②,得
(1,2)?(p,q)=(p+2q,2p-q),
∵(1,2)?(p,q)=(11,2),
∴(p+2q,2p-q)=(11,2),
由规定①,得
,解得
,
由规定③,可知
(1,2)θ(p,q)
=(1,2)θ(3,4)
=(1-3,2-4)
=(-2,-2).
故选A.
(1,2)?(p,q)=(p+2q,2p-q),
∵(1,2)?(p,q)=(11,2),
∴(p+2q,2p-q)=(11,2),
由规定①,得
|
|
由规定③,可知
(1,2)θ(p,q)
=(1,2)θ(3,4)
=(1-3,2-4)
=(-2,-2).
故选A.
点评:本题考查了有理数无理数的概念与运算.关键是理解规定运算,依照规定运算的要求,依次计算.

练习册系列答案
相关题目
 和
和 ,规定:当
,规定:当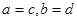 时,有
时,有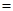
 ”为:
”为: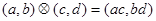 ;运算“
;运算“ ”为:
”为: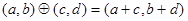 .设
.设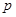 、
、 都是实数,若
都是实数,若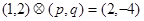 ,则
,则 .
.