题目内容
15、对于任意的两个实数对(a,b)和(c,d),规定:当a=c,b=d时,有(a,b)=(c,d);运算“×”为:(a,b)×(c,d)=(ac,bd);运算“+”为:(a,b)+(c,d)=(a+c,b+d).设p,q都是实数,若(1,2)×(p,q)=(2,-4),则(1,2)+(p,q)=
(3,0)
.分析:首先根据运算“×”的规定,由(1,2)×(p,q)=(2,-4),求出p、q的值,再根据运算“+”的规定,得出结果.
解答:解:∵(1,2)×(p,q)=(p,2q)=(2,-4),
∴p=2,q=-2;
∴(1,2)+(p,q)=(1,2)+(2,-2)=(1+2,2-2)=(3,0).
故填(3,0)
∴p=2,q=-2;
∴(1,2)+(p,q)=(1,2)+(2,-2)=(1+2,2-2)=(3,0).
故填(3,0)
点评:此题是定义新运算题型.考查了学生的阅读理解能力及知识的迁移能力.理解新规则是解题的关键.

练习册系列答案
相关题目
 和
和 ,规定:当
,规定:当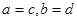 时,有
时,有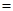
 ”为:
”为: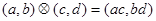 ;运算“
;运算“ ”为:
”为: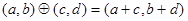 .设
.设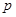 、
、 都是实数,若
都是实数,若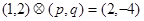 ,则
,则 .
.