题目内容
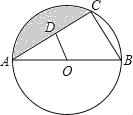
【题目】如图,AB是⊙O的直径,OD∥BC,∠A=30°,CD=2.
求:(1)弦BC的长;
(2)图中阴影部分的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)根据圆周角定理得∠ACB=90°,再由OD∥BC得∠ADO=90°,则根据垂径定理得到AD=DC=2,即AC=4,然后根据含30°的直角三角形三边的关系可计算出BC;
(2)先得到OD=![]() BC=
BC=![]() ,再计算出半径,然后根据扇形面积公式和阴影部分的面积=S扇形OAC-S△OAC进行计算即可.
,再计算出半径,然后根据扇形面积公式和阴影部分的面积=S扇形OAC-S△OAC进行计算即可.
试题解析:(1)∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD∥BC,
∴∠ADO=90°,
∴OD⊥AC,
∴AD=DC=2,
∴AC=4,
∵∠A=30°,
∴BC=![]() AC=
AC=![]() ;
;
(2)连结OC,如图,
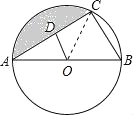
∵OD为△ACB的中位线,
∴OD=![]() BC=
BC=![]() ,,
,,
在Rt△ACB中,∠A=30°,
∴∠B=60°,
∴OC=BC=![]() ,∠AOC=2∠B=120°,
,∠AOC=2∠B=120°,
∴阴影部分的面积=S扇形OAC-S△OAC
=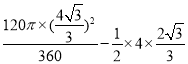
=![]() .
.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
【题目】我市为了解中学生的视力情况,对某校三个年级的学生视力进行了抽样调查,得到不完整的统计表与扇形统计图如下,其中扇形统计图的圆心角α为36°,x表示视力情况,根据上面提供的信息,回答下列问题:
分组 | 视力情况 | 频数 | 频率 |
A | 4.0≤x<4.3 | 20 | |
B | 4.3≤x<4.6 | 0.35 | |
C | 4.6≤x<4.9 | 50 | |
D | x≥4.9 |
(1)此次共调查了 人;
(2)请将表格补充完整;
(3)这组数据的中位数落在 组内;
(4)扇形统计图中“D组”的扇形所对的圆心角的度数是 .