题目内容
【题目】探究:如图①,在矩形ABCD中,AB=3,AD=4,点P是对角线AC上的一点,过点P分别作AB、AD的平行线,交BC、CD于点M、N,求![]() 的值;
的值;
应用:如图②,在矩形ABCD中,AB=3,AD=4,点P是对角线AC上的一点,Rt△PEF的两条直角边PE、PF分别交BC、CD于点M、N,则![]() = .
= .

【答案】![]() ;
;![]()
【解析】
试题分析:探究:首先证明PN=MC,由PM∥AB,推出![]() ,即
,即![]() ,由此即可解决问题.
,由此即可解决问题.
应用:先过P作PG⊥BC于G,作PH⊥CD于H,判定△PGM∽△PHN,再根据相似三角形的性质以及探究的结论即可解决问题;
试题解析:探究:解:如图①中,
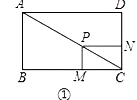
∵四边形ABCD是矩形,
∴∠B=∠DCB=90°,AD=BC=4
∵PM⊥BC,PN⊥CD,
∴∠PMC=∠PNC=90°,
∴四边形PMCN是矩形,
∴PC=CM,
∵∠PMC=∠B=90°,
∴PM∥AB,
∴△CPM∽△CAB,
∴![]() ,即
,即![]() ,
,
∵AB=3,BC=4
∴![]() =
=![]()
应用:解:如图②中,过P作PG⊥BC于G,作PH⊥CD于H,则∠PGM=∠PHN=90°,∠GPH=90°,

∵Rt△PEF中,∠FPE=90°
∴∠GPM=∠HPN
∴△PGM∽△PHN
∴![]() ,
,
由条件可知,![]() =
=![]() ,
,
∴![]() =
=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
