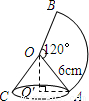题目内容
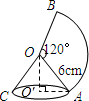 如图,将一个半径为6cm,圆心角为120°的扇形薄铁皮AOB卷成圆锥AOC的侧面(接缝无重叠,无缝隙),O′为圆锥的底面圆心,则O′A=
如图,将一个半径为6cm,圆心角为120°的扇形薄铁皮AOB卷成圆锥AOC的侧面(接缝无重叠,无缝隙),O′为圆锥的底面圆心,则O′A=分析:半径为6cm,圆心角为120°的扇形的弧长是
=4π,圆锥的底面周长等于侧面展开图的扇形弧长,因而圆锥的底面周长是4π,设圆锥的底面半径是r,则得到2πr=4π,解得:r=2.
| 120π•6 |
| 180 |
解答:解:
=4π,
圆锥的底面周长等于侧面展开图的扇形弧长,
因而圆锥的底面周长是4πcm,
设圆锥的底面半径是r,
则得到2πr=4π,
解得:r=2cm.
| 120π•6 |
| 180 |
圆锥的底面周长等于侧面展开图的扇形弧长,
因而圆锥的底面周长是4πcm,
设圆锥的底面半径是r,
则得到2πr=4π,
解得:r=2cm.
点评:本题综合考查有关扇形和圆锥的相关计算.
解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:
(1)圆锥的母线长等于侧面展开图的扇形半径;
(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.
解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:
(1)圆锥的母线长等于侧面展开图的扇形半径;
(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
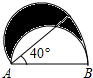 如图,将一个半径为4cm的半圆绕直径AB的一个端点A旋转40°,那么,图中阴影部分的面积为
如图,将一个半径为4cm的半圆绕直径AB的一个端点A旋转40°,那么,图中阴影部分的面积为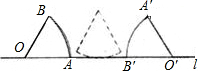 如图,将一个半径为3,圆心角为60°的扇形AOB,如图放置在直线l上(OA与直线l重合),然后将这个扇形在直线l上无摩擦滚动至O′A′B′的位置,在这个过程中,点O运动到点O′的路径长度为( )
如图,将一个半径为3,圆心角为60°的扇形AOB,如图放置在直线l上(OA与直线l重合),然后将这个扇形在直线l上无摩擦滚动至O′A′B′的位置,在这个过程中,点O运动到点O′的路径长度为( )