题目内容
在平面直角坐标系xOy中,已知点A(0,1),B(1,2),点P在x轴上运动,当点P到A、B两点距离之差的绝对值最大时,点P的坐标是 .
(﹣1,0)
分析:由三角形两边之差小于第三边可知,
当A、B、P三点不共线时,由三角形三边关系|PA﹣PB|<AB;
当A、B、P三点共线时,∵A(0,1),B(1,2)两点都在x轴同侧,∴|PA﹣PB|=AB。
∴|PA﹣PB|≤AB。
∴本题中当点P到A、B两点距离之差的绝对值最大时,点P在直线AB上。
设直线AB的解析式为y=kx+b,
∵A(0,1),B(1,2),∴
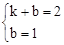 ,解得
,解得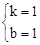 。
。∴直线AB的解析式为y=x+1。
令y=0,得0=x+1,解得x=﹣1。
∴点P的坐标是(﹣1,0)。

练习册系列答案
相关题目
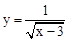 中自变量x的取值范围是 .
中自变量x的取值范围是 . 中自变量
中自变量 的取值范围是
的取值范围是







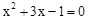 的根可视为函数
的根可视为函数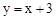 的图象与函数
的图象与函数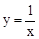 的图象交点的横坐标,则方程
的图象交点的横坐标,则方程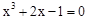 的实根x0所在的范围是
的实根x0所在的范围是



 中,自变量x的取值范围是 。
中,自变量x的取值范围是 。 中,自变量x的取值范围是 .
中,自变量x的取值范围是 .