题目内容
 如图,某公园有一块矩形草地ABCD,矩形草地的边及对角线BD是小路,BC长40米,CD长30米.妈妈站在A处,亮亮沿着小路B?C?D?B跑步.在跑步过程中,亮亮与妈妈之间的最短距离为
如图,某公园有一块矩形草地ABCD,矩形草地的边及对角线BD是小路,BC长40米,CD长30米.妈妈站在A处,亮亮沿着小路B?C?D?B跑步.在跑步过程中,亮亮与妈妈之间的最短距离为分析:过A向BD作垂线段,垂线段长即为最短距离.
解答:解:比较可得最短的应该是A到BD边的高线,因为BC=40米,CD=30米,
由勾股定理得,BD=50米,
由面积公式得,
AB•AD=
BD•高,
解得:高为24米,
即亮亮与妈妈之间的最短距离为24米.
由勾股定理得,BD=50米,
由面积公式得,
| 1 |
| 2 |
| 1 |
| 2 |
解得:高为24米,
即亮亮与妈妈之间的最短距离为24米.
点评:此题考查了学生对勾股定理在实际生活中的运用能力及三角形的面积公式的掌握情况.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
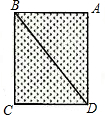 如图,某公园有一块矩形草地ABCD,矩形草地的边及对角线BD是小路,BC长40米,CD长30米,妈妈站在A处,亮亮沿着小路B-C-D-B跑步,在跑步过程中,亮亮与妈妈之间的最短距离为( )
如图,某公园有一块矩形草地ABCD,矩形草地的边及对角线BD是小路,BC长40米,CD长30米,妈妈站在A处,亮亮沿着小路B-C-D-B跑步,在跑步过程中,亮亮与妈妈之间的最短距离为( )

