Question

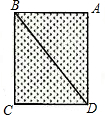如图，某公园有一块矩形草地ABCD，矩形草地的边及对角线BD是小路，BC长40米，CD长30米，妈妈站在A处，亮亮沿着小路B-C-D-B跑步，在跑步过程中，亮亮与妈妈之间的最短距离为（　　）

• A、30米
• B、40米
• C、50米
• D、24米

Answer 1

分析：作AE⊥BD，过A点作直线的垂线，则垂线是点与直线上的点的最短距离，所以亮亮与妈妈的最短距离为AE，直角△ABD中，已知AB，AD，根据勾股定理可以求BD，根据面积法可以求AE．

解答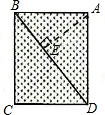：解：作AE⊥BD，
则亮亮在E点时，亮亮与妈妈的距离最短，
在直角△ABD中，AB=30米，BC=40米，
则BD=

AB2+AD2

=50米，
△ABD的面积为

1

2

AB×AD=

1

2

BD×AE，
∴AE=

30×40

50

米=24米．
故选D．

点评：本题考查了勾股定理在实际生活中的运用，考查了直角三角形面积的计算，本题中根据面积法计算AE的长是解题的关键．