题目内容
 我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别为a、b,那么(a+b)2的值是
我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边分别为a、b,那么(a+b)2的值是分析:根据正方形的面积公式以及勾股定理,结合图形进行分析发现:大正方形的面积即直角三角形斜边的平方13,也就是两条直角边的平方和是13,四个直角三角形的面积和是大正方形的面积减去小正方形的面积即2ab=12.根据完全平方公式即可求解.
解答:解:根据题意,结合勾股定理a2+b2=13,
四个三角形的面积=4×
ab=13-1,
∴2ab=12,
联立解得:(a+b)2=13+12=25.
故答案为:25.
四个三角形的面积=4×
| 1 |
| 2 |
∴2ab=12,
联立解得:(a+b)2=13+12=25.
故答案为:25.
点评:注意观察图形:发现各个图形的面积和a,b的关系.

练习册系列答案
相关题目

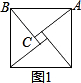

 如图是2002年8月在北京召开的国际数学家大会的会标,它取材于我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形和一个小正方形的拼成的大正方形,如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短边为a,较长边为b,那么(a+b)2的值是
如图是2002年8月在北京召开的国际数学家大会的会标,它取材于我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形和一个小正方形的拼成的大正方形,如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短边为a,较长边为b,那么(a+b)2的值是 我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a、b,试求:(a+b)2 的值.
我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为a、b,试求:(a+b)2 的值. 我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是49,小正方形的面积4,直角三角形的两直角边长分别为a,b,那么下列结论正确的有( )个.
我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成一个大正方形(如图所示).如果大正方形的面积是49,小正方形的面积4,直角三角形的两直角边长分别为a,b,那么下列结论正确的有( )个.