Question

【题目】在中，D，E，F分别是三边，，上的中点，连接，，，，已知．

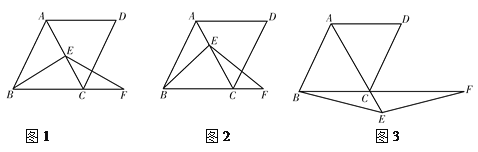
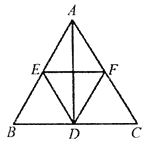
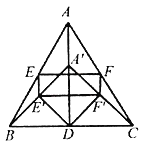
（1）观察猜想：如图，当时，①四边形的对角线与的数量关系是________；②四边形的形状是_______；

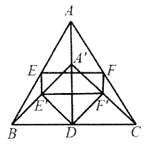
（2）数学思考：如图，当时，（1）中的结论①，②是否发生变化？若发生变化，请说明理由；

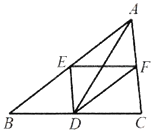
（3）拓展延伸：如图，将上图的点A沿向下平移到点，使得，已知，分别为，的中点，求四边形与四边形的面积比．

Answer 1

【答案】（1）①，②平行四边形；（2）结论①不变，结论②由平行四边形变为菱形，理由详见解析；（3）

【解析】

（1）根据三角形中位线定理，即可得出，进而得解；由三角形中位线定理得出DE∥AC, ,即可判定为平行四边形；

（2）由中位线定理得出，，，然后根据，得出，，即可判定平行四边形是菱形；

（3）首先设，，根据等腰直角三角形的性质，得出，进而得出，然后由三角形中位线定理得，，经分析可知：，且和互相垂直平分，即可得出四边形为正方形，又由，，，得出四边形为矩形，即可得出面积比.

解：（1）①，②平行四边形；

由已知条件和三角形中位线定理，得

又∵

∴

②由三角形中位线定理得，

DE∥AC, ,

∴四边形是平行四边形；

（2）结论①不变，结论②由平行四边形变为菱形，

四边形是菱形的理由是：

∵，都是的中位线，

∴，

∴四边形是平行四边形

∵是的中位线，

∴

∵

∴，

∴

∴平行四边形是菱形．

（3）设，

当，是等腰直角三角形，

∴

∴

由三角形中位线定理得，，

∴，且和互相垂直平分

∴四边形为正方形，

∵，EF⊥AD，

∴

∴

又∵，

∴四边形为矩形，

∴，

∴所求面积比为