题目内容
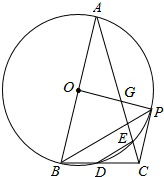 (2013•工业园区二模)如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,过点B作BP平行于DE,交⊙O于点P,连结CP、OP,OP交AC于点G.
(2013•工业园区二模)如图,在△ABC中,AB=AC,∠A=30°,以AB为直径的⊙O交BC于点D,交AC于点E,连结DE,过点B作BP平行于DE,交⊙O于点P,连结CP、OP,OP交AC于点G.(1)BD=DC吗?说明理由;
(2)求∠BOP的度数;
(3)求证:CP是⊙O的切线;
(4)请直接写出
| AB•BC |
| PC2 |
| 6 |
| 2 |
| 6 |
| 2 |
分析:(1)连接AD,由圆周角定理可知∠ADB=90°,再根据等腰三角形的性质得到BD=DC;
(2)根据等腰三角形的性质得到AD平方∠BAC,即∠BAD=∠CAD,根据圆周角定理得
=
,则BD=DE,所以BD=DE=DC,得到∠DEC=∠DCE,在等腰△ABC中可计算出∠ABC=75°,故∠DEC=75°,再由三角形内角和定理得出∠EDC的度数,再根据BP∥DE可知∠PBC=∠EDC=30°,进而得出∠ABP的度数,然后利用OB=OP,可知∠OBP=∠OPB,由三角形内角和定理即可得出∠BOP=90°;
(3)设OP交AC于点G,由∠BOP=90°可知∠AOG=90°,在Rt△AOG中,由∠OAG=30°可得
=
,由于
=
=
,则
=
,根据比例性质得
=
,而∠AGO=∠CGP,根据三角形相似的判定可得到△AOG∽△CPG,由相似三角形形的性质可知∠GPC=∠AOG=90°,然后根据切线的判定定理即可得到CP是⊙O的切线;
(4)作CH⊥BP于H,易△PHC为等腰直角三角形,设HC=x,则PH=x,PC=
x,在Rt△BHC中,根据含30度的直角三角形三边的关系得BC=2x,BH=
x,则PB=(
+1)x,在Rt△OPB中,根据等腰直角三角形的性质得OB=
x,则AB=(
+
)x,然后计算
的值.
(2)根据等腰三角形的性质得到AD平方∠BAC,即∠BAD=∠CAD,根据圆周角定理得
 |
| BD |
 |
| DE |
(3)设OP交AC于点G,由∠BOP=90°可知∠AOG=90°,在Rt△AOG中,由∠OAG=30°可得
| OG |
| AG |
| 1 |
| 2 |
| OP |
| AC |
| OP |
| AB |
| 1 |
| 2 |
| OP |
| AC |
| OG |
| AG |
| OG |
| AG |
| GP |
| GC |
(4)作CH⊥BP于H,易△PHC为等腰直角三角形,设HC=x,则PH=x,PC=
| 2 |
| 3 |
| 3 |
| ||||
| 2 |
| 6 |
| 2 |
| AB•BC |
| PC2 |
解答:解:(1)BD=DC.理由如下:连接AD,
∵AB是直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=DC;
 (2)∵AD是等腰△ABC底边上的中线,
(2)∵AD是等腰△ABC底边上的中线,
∴∠BAD=∠CAD,
∴
=
,
∴BD=DE.
∴BD=DE=DC,
∴∠DEC=∠DCE,
△ABC中,AB=AC,∠A=30°,
∴∠DCE=∠ABC=
(180°-30°)=75°,
∴∠DEC=75°,
∴∠EDC=180°-75°-75°=30°,
∵BP∥DE,
∴∠PBC=∠EDC=30°,
∴∠ABP=∠ABC-∠PBC=75°-30°=45°,
∵OB=OP,
∴∠OBP=∠OPB=45°,
∴∠BOP=90°;
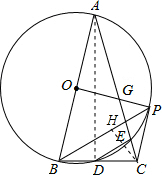
(3)设OP交AC于点G,如图,则∠AOG=∠BOP=90°,
在Rt△AOG中,∠OAG=30°,
∴
=
,
又∵
=
=
,
∴
=
,
∴
=
,
又∵∠AGO=∠CGP,
∴△AOG∽△CPG,
∴∠GPC=∠AOG=90°,
∴OP⊥PC,
∴CP是⊙O的切线;
(4)作CH⊥BP于H,如图,∵∠OPC=90°,∠OPB=45°,
∴∠HPC=45°,
设HC=x,则PH=x,PC=
x,
在Rt△BHC中,∠HBP=30°,
∴BC=2x,BH=
x,
∴PB=
x+x=(
+1)x,
在Rt△OPB中,OB=
PB=
x,
∴AB=(
+
)x,
∴
=
=
+
.
故答案为
+
.
∵AB是直径,
∴∠ADB=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=DC;
 (2)∵AD是等腰△ABC底边上的中线,
(2)∵AD是等腰△ABC底边上的中线,∴∠BAD=∠CAD,
∴
 |
| BD |
 |
| DE |
∴BD=DE.
∴BD=DE=DC,
∴∠DEC=∠DCE,
△ABC中,AB=AC,∠A=30°,
∴∠DCE=∠ABC=
| 1 |
| 2 |
∴∠DEC=75°,
∴∠EDC=180°-75°-75°=30°,
∵BP∥DE,
∴∠PBC=∠EDC=30°,
∴∠ABP=∠ABC-∠PBC=75°-30°=45°,
∵OB=OP,
∴∠OBP=∠OPB=45°,
∴∠BOP=90°;
(3)设OP交AC于点G,如图,则∠AOG=∠BOP=90°,
在Rt△AOG中,∠OAG=30°,
∴
| OG |
| AG |
| 1 |
| 2 |
又∵
| OP |
| AC |
| OP |
| AB |
| 1 |
| 2 |
∴
| OP |
| AC |
| OG |
| AG |
∴
| OG |
| AG |
| GP |
| GC |
又∵∠AGO=∠CGP,
∴△AOG∽△CPG,
∴∠GPC=∠AOG=90°,
∴OP⊥PC,
∴CP是⊙O的切线;
(4)作CH⊥BP于H,如图,∵∠OPC=90°,∠OPB=45°,
∴∠HPC=45°,
设HC=x,则PH=x,PC=
| 2 |
在Rt△BHC中,∠HBP=30°,
∴BC=2x,BH=
| 3 |
∴PB=
| 3 |
| 3 |
在Rt△OPB中,OB=
| ||
| 2 |
| ||||
| 2 |
∴AB=(
| 6 |
| 2 |
∴
| AB•BC |
| PC2 |
(
| ||||
| 2x2 |
| 6 |
| 2 |
故答案为
| 6 |
| 2 |
点评:本题考查了圆的综合题:掌握运用切线的判定定理证明圆的切线;运用圆周角定理和相似三角形的判定与性质解决圆中角度与线段的计算;同时记住等腰直角三角形的性质以及含30度的直角三角形三边的关系.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 (2013•工业园区二模)某班50名同学积极响应“为雅安地震灾区献爱心捐款活动”,并将所捐款情况统计并制成统计图,根据图中信息,捐款金额的众数和中位数分别是
(2013•工业园区二模)某班50名同学积极响应“为雅安地震灾区献爱心捐款活动”,并将所捐款情况统计并制成统计图,根据图中信息,捐款金额的众数和中位数分别是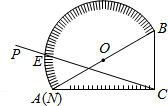 (2013•工业园区二模)如图,量角器的直径与直角三角板ABC的斜边AB重合,其中AB=8cm,量角器O刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第35秒时,点E在量角器上对应划过的
(2013•工业园区二模)如图,量角器的直径与直角三角板ABC的斜边AB重合,其中AB=8cm,量角器O刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,第35秒时,点E在量角器上对应划过的 (2013•工业园区二模)如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.当线段AM最短时,重叠部分的面积是
(2013•工业园区二模)如图,在△ABC中,已知AB=AC=5,BC=6,且△ABC≌△DEF,将△DEF与△ABC重合在一起,△ABC不动,△DEF运动,并满足:点E在边BC上沿B到C的方向运动,且DE始终经过点A,EF与AC交于M点.当线段AM最短时,重叠部分的面积是