题目内容
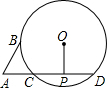如图，AB切⊙O于点B，AD交⊙O于点C、D，OP⊥CD于点P．若AB=4cm，AD=8cm，⊙O的半径为5cm，则OP=分析：由于AB是⊙O的切线，可首先由切割线定理求出AC的长，即可得到CD的长，进而可由垂径定理求出PC的长；连接OC，在Rt△OCP中，由勾股定理即可求得OP的值．
解答：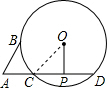
解：连接OC；
∵AB切⊙O于B，
∴AB2=AC•AD，即AC=AB2÷AD=2cm；
∴CD=AD-AC=6cm；
Rt△OCP中，OC=5cm，PC=3cm；
由勾股定理，得：OP=
=4cm．
故答案为：4．
解：连接OC；∵AB切⊙O于B，
∴AB2=AC•AD，即AC=AB2÷AD=2cm；
∴CD=AD-AC=6cm；
Rt△OCP中，OC=5cm，PC=3cm；
由勾股定理，得：OP=
| OC2-CP2 |
故答案为：4．
点评：此题主要考查了切割线定理、垂径定理及勾股定理的综合运用；能够由切割线定理求出CD的长，是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
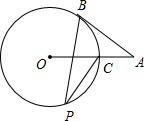已知：如图，AB切⊙O于点B，OA与⊙O交于点C，点P在⊙O上，若∠BAC=40°，则∠BPC的度数为（ ）| A、20° | B、25° | C、30° | D、40° |
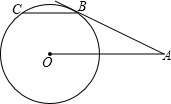如图，AB切⊙O于点B，OA=2| 3 |
A、
| ||||
B、
| ||||
| C、π | ||||
D、
|
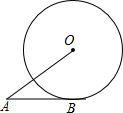如图，AB切⊙O于点B，AB=4cm，AO=6cm，则⊙O的半径为
（2012•西藏）如图，AB切⊙O于点B，延长AO交⊙O于点C，连接BC．若∠A=40°，则∠C=（ ）
（2012•广东模拟）如图，AB切⊙O于点A，OD⊥弦AC于点D，延长OD，交AB于点B，若∠O=60°，AC=6cm，则AB=