题目内容
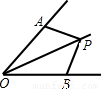
 (2012•西藏)如图,AB切⊙O于点B,延长AO交⊙O于点C,连接BC.若∠A=40°,则∠C=( )
(2012•西藏)如图,AB切⊙O于点B,延长AO交⊙O于点C,连接BC.若∠A=40°,则∠C=( )分析:根据切线的性质判定∠ABO=90°,然后在直角△ABO中利用直角三角形的性质求得∠AOB=50°;最后根据圆周角定理来求∠C的度数.
解答: 解:∵AB切⊙O于点B,
解:∵AB切⊙O于点B,
∴OB⊥AB,即∠ABO=90°,
∴∠AOB=50°(直角三角形中的两个锐角互余),
又∵点C在AO的延长线上,且在⊙O上,
∴∠C=
∠AOB=25°(同弧所对的圆周角是所对的圆心角的一半).
故选B.
 解:∵AB切⊙O于点B,
解:∵AB切⊙O于点B,∴OB⊥AB,即∠ABO=90°,
∴∠AOB=50°(直角三角形中的两个锐角互余),
又∵点C在AO的延长线上,且在⊙O上,
∴∠C=
| 1 |
| 2 |
故选B.
点评:本题考查了圆周角定理、切线的性质.定理成立的条件是“同一条弧所对的”两种角,在运用定理时不要忽略了这个条件,把不同弧所对的圆周角与圆心角错当成同一条弧所对的圆周角和圆心角.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 (2012•西藏)如图,小明从纸上剪下一个圆形和一个扇形纸片,用它们恰好能围成一个圆锥模型.若圆的半径为1,扇形的圆心角为120°,则此扇形的半径为
(2012•西藏)如图,小明从纸上剪下一个圆形和一个扇形纸片,用它们恰好能围成一个圆锥模型.若圆的半径为1,扇形的圆心角为120°,则此扇形的半径为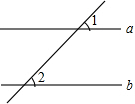 (2012•西藏)如图,已知直线a∥b,∠1=50°,则∠2=
(2012•西藏)如图,已知直线a∥b,∠1=50°,则∠2=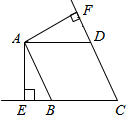 (2012•西藏)如图,四边形ABCD是菱形,AE⊥BC交CB的延长线于点E,AF⊥CD交CD的延长线于点F.求证:AE=AF.
(2012•西藏)如图,四边形ABCD是菱形,AE⊥BC交CB的延长线于点E,AF⊥CD交CD的延长线于点F.求证:AE=AF.