题目内容
如图CD是等腰三角形ABC的对称轴，DE⊥CB于E，∠B=55°，则∠CDE的度数是
- A.55°
- B.35°
- C.45°
- D.30°
A
分析：要求角的度数，由已知开始思考，在Rt△CDB中，DE⊥CB，则∠CDE和∠B同为∠BDE的余角，所以这两角相等，由此可求出∠CDE的度数．
解答：∵CD是等腰三角形ABC的对称轴，
∴CD⊥AB，即∠CDB=90°；
Rt△CDB中，DE⊥BC；
∴∠CDE=∠B=90°-∠BDE；
即∠CDE=55°．
故选A．
点评：此题考查的是等腰三角形的性质：等腰三角形顶角平分线、底边的中线和高线，互相重合．进行角的等量代换是正确解答本题的关键．
分析：要求角的度数，由已知开始思考，在Rt△CDB中，DE⊥CB，则∠CDE和∠B同为∠BDE的余角，所以这两角相等，由此可求出∠CDE的度数．
解答：∵CD是等腰三角形ABC的对称轴，
∴CD⊥AB，即∠CDB=90°；
Rt△CDB中，DE⊥BC；
∴∠CDE=∠B=90°-∠BDE；
即∠CDE=55°．
故选A．
点评：此题考查的是等腰三角形的性质：等腰三角形顶角平分线、底边的中线和高线，互相重合．进行角的等量代换是正确解答本题的关键．
练习册系列答案
相关题目
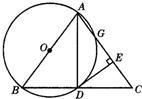50、如图，以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D，交AC于点G，连接AD，并过点D作DE⊥AC，垂足为E．根据以上条件写出三个正确结论（除AB=AC，AO=BO，∠ABC=∠ACB外）是：
8、如图CD是等腰三角形ABC的对称轴，DE⊥CB于E，∠B=55°，则∠CDE的度数是（ ）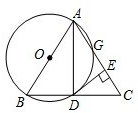
如图，以等腰三角形ABC的一腰AB为直径的⊙O交BC于点D，交AC于点G，连接AD，并过点D作DE⊥AC，垂足为E．根据以上条件写出三个正确结论（除AB=AC，AO=BO，∠ABC=∠ACB外）是：
如图，在等腰三角形ABC中，两底角的平分线BE和CD相交于点0，则△OBC是