题目内容
如图，两个正方形的边长均为2，其中一个正方形的顶点在另一个正方形的中心，则两个正方形重合部分的面积为________．
1
分析：过ABCD的中心O作OM⊥CD于M，作ON⊥BC于N，则易证△OEM≌△OFN，则四边形OECF的面积就等于正方形OMCN的面积，根据已知可求得OMCN的面积，从而可得到重合部分的面积．
解答：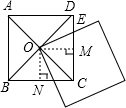
解：过ABCD的中心O作OM⊥CD于M，作ON⊥BC于N，则易证△OEM≌△OFN，则四边形OECF的面积就等于正方形OMCN的面积，正方形ABCD的边长是2，则OMCN的面积是1，因而图形中重合部分的面积为1．
故答案为1．
点评：此题主要考查正方形对角线相等平分垂直的性质的运用．
分析：过ABCD的中心O作OM⊥CD于M，作ON⊥BC于N，则易证△OEM≌△OFN，则四边形OECF的面积就等于正方形OMCN的面积，根据已知可求得OMCN的面积，从而可得到重合部分的面积．
解答：
解：过ABCD的中心O作OM⊥CD于M，作ON⊥BC于N，则易证△OEM≌△OFN，则四边形OECF的面积就等于正方形OMCN的面积，正方形ABCD的边长是2，则OMCN的面积是1，因而图形中重合部分的面积为1．故答案为1．
点评：此题主要考查正方形对角线相等平分垂直的性质的运用．
练习册系列答案
相关题目
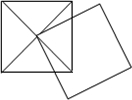如图，两个正方形的边长均为1，其中一个正方形的顶点在另一个正方形的中心，则两个正方形重合部分的面积为
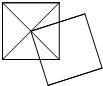4、如图，两个正方形的边长均为2，其中一个正方形的顶点在另一个正方形的中心，则两个正方形重合部分的面积为
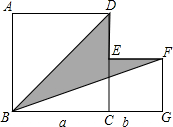如图，两个正方形的边长分别为a和b，如果a+b=10，ab=20，那么：
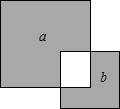如图，两个正方形的边长分别为5与3，两个阴影部分的面积分别为a、b（a＞b），则