题目内容
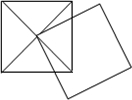如图，两个正方形的边长均为1，其中一个正方形的顶点在另一个正方形的中心，则两个正方形重合部分的面积为分析：根据题意可以推出△OBG≌△ODH，所以重合部分的面积为△OBD的面积
解答：
解：∵四边形ABDC与OEFM都是正方形，
∴∠OBG=∠ODH=45°，OB=OD，∠BOG=∠DOH=90°-∠DOG，
∴△OBG≌△ODH，
又∵两个正方形的边长都为1，
∴OB=OD=
，
∴四边形OGHD的面积=S△OGD+S△ODH，
∴四边形OGHD的面积=S△OGD+S△OBG=S△OBD，
∴四边形OGHD的面积=
．
故答案为：
．
解：∵四边形ABDC与OEFM都是正方形，∴∠OBG=∠ODH=45°，OB=OD，∠BOG=∠DOH=90°-∠DOG，
∴△OBG≌△ODH，
又∵两个正方形的边长都为1，
∴OB=OD=
| ||
| 2 |
∴四边形OGHD的面积=S△OGD+S△ODH，
∴四边形OGHD的面积=S△OGD+S△OBG=S△OBD，
∴四边形OGHD的面积=
| 1 |
| 4 |
故答案为：
| 1 |
| 4 |
点评：本题主要考查了正方形的性质定理、三角形的面积、全等三角形的判定和性质．解题关键在于找到全等三角形进行代换．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
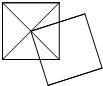4、如图，两个正方形的边长均为2，其中一个正方形的顶点在另一个正方形的中心，则两个正方形重合部分的面积为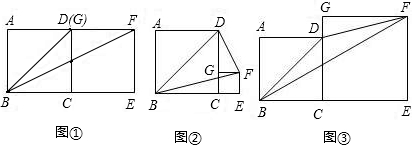
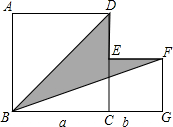如图，两个正方形的边长分别为a和b，如果a+b=10，ab=20，那么：
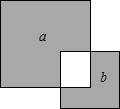如图，两个正方形的边长分别为5与3，两个阴影部分的面积分别为a、b（a＞b），则