题目内容
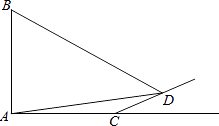
【题目】如图,在长方形ACDF中,AC=DF,点B在CD上,点E在DF上,BC=DE=a,AC=BD=b,AB=BE=c,且AB⊥BE.

(1)用两种不同的方法表示长方形ACDF的面积S
方法一:S=
方法二:S=
(2)求a,b,c之间的等量关系(需要化简)
(3)请直接运用(2)中的结论,求当c=5,a=3,S的值
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)28
;(3)28
【解析】
(1)方法一,根据矩形的面积公式就可以直接表示出S;
方法二,根据矩形的面积等于四个三角形的面积之和求出结论即可;
(2)根据方法一与方法二的S相等建立等式就可以表示出a,b,c之间的等量关系;
(3)先由(2)的结论求出b的值,然后代入S的解析式就可以求出结论.
(1)由题意,得:
方法一:![]() ;
;
方法二:![]() ;
;
故答案为:![]() ,
,![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)∵![]() ,且
,且![]() ,
,![]() ,
,
∴![]() ,
,
∴![]()
=28.
答:S的值为28.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目