题目内容
如图，用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上，若四周下垂的最大长度相等，则桌布下垂的最大长度x为（ ）
A． | B． | C． | D． |
B．
试题分析：作出图象，把实际问题转化成数学问题，求出弦心距，再用半径减弦心距即可：
如图，正方形ABCD是圆内接正方形，BD=a，点O是圆心，也是正方形的对角线的交点，则OB=
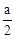，△BOC是等腰直角三角形，
作OF⊥BC，垂足为F，由垂径定理知，点F是BC的中点，∴OF=OBsin45°=
.∴
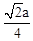.故选B．
练习册系列答案
相关题目
如图，⊙O是Rt△ABC的外接圆，∠ABC=90°，弦BD=BA，AB=12，BC=5，BE⊥DC交DC的延长线于点E.
（1）求证：∠BCA=∠BAD；
（2）求DE的长；
（3）求证:BE是⊙O的切线.
（1）求证：∠BCA=∠BAD；
（2）求DE的长；
（3）求证:BE是⊙O的切线.
于D，点A是优弧
上的动点(不与B、C重合)，BC=
，ED=2．
，求弦MN的长．
的两个根，则两圆的位置关系是（ ）