Question

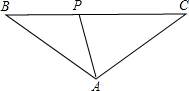已知：如图，△ABC中，AB=AC=10m，BC=16m，现点P从B点出发，沿BC向点C运动，运动速度为

1

4

m/s．问P点经过几秒后，线段AP把△ABC分割而得的三角形中至少有一个是直角三角形？

Answer 1

分析：本题需分∠APC=90°∠PAC=90°∠PAB=90°三种情况讨论，再根据BP、CP、AP、AB以及BC边上的高AD之间的关系列出方程，求出解即可．

解答：解：设P点经过t秒后，线段AP把△ABC分割而得的三角形中至少有一个是直角三角形
此时BP=

1

4

t，PC=16-

1

4

t

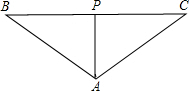
（1）当∠APC=90°时，AP⊥BC，
∵AB=AC，AP⊥BC，
∴BP=CP=

1

2

BC=8，
∴

1

4

t=8，
∴t=32；

（2）当∠PAC=90°时，过A作AD⊥BC

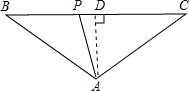
∵AB=AC，AD⊥BC，
∴BD=CD=

1

2

BC=8，
∴PD=BD-BP=8-

1

4

t，
在Rt△ADC中，AD²=AC²-CD²，
∴AD=6，
在Rt△PAC中，AP²=CP²-AC²，
在Rt△ADP中，AP²=AD²+PD²，
∴CP²-AC²=AD²+PD²，
∴(16-

1

4

t)2-100=(8-

1

4

t)2+36，
解得t=14；

（3）当∠PAB=90°时，过A作AE⊥BC

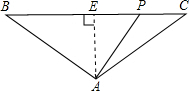
∵AB=AC，AD⊥BC，
∴BE=CE=

1

2

BC=8，
∴PE=BP-BE=

1

4

t-8，
在Rt△AEC中，AE²=AC²-CE²，
∴AE=6，
在Rt△PAB中，AP²=BP²-AB²，
在Rt△AEP中，AP²=AE²+PE²，
∴BP²-AB²=AE²+PE²，
∴(

1

4

t)2-100=(

1

4

t-8)2+36，
解得t=50．
答：P点经过14秒或32秒或50秒后，线段AP把△ABC分割而得的三角形中至少有一个是直角三角形．

点评：本题解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程，再求解．