题目内容
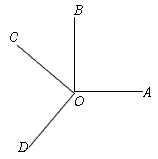
 如图,∠AOB=42゜,∠BOC=86゜,OD为∠AOC的平分线,求∠BOD的度数.
如图,∠AOB=42゜,∠BOC=86゜,OD为∠AOC的平分线,求∠BOD的度数.分析:首先求得∠AOC的度数,根据角平分线的定义求得∠AOD,然后根据∠BOD=∠AOD-∠AOB求解.
解答:解:∵∠AOB=42°,∠BOC=86°,
∴∠AOC=∠AOB+∠BOC=42°+86°=128゜.
∵OD平分∠AOC,
∴∠AOD=
∠AOC=
×128°=64°.
∴∠BOD=∠AOD-∠AOB=64゜-42゜=22°.
答:∠BOD的度数是22゜.
∴∠AOC=∠AOB+∠BOC=42°+86°=128゜.
∵OD平分∠AOC,
∴∠AOD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BOD=∠AOD-∠AOB=64゜-42゜=22°.
答:∠BOD的度数是22゜.
点评:本题考查了角度的计算,正确理解角平分线的定义,求得∠AOD是关键.

练习册系列答案
相关题目
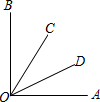 如图,∠AOB=90°,∠BOC=42°,OD平分∠AOC.求∠AOD的度数.
如图,∠AOB=90°,∠BOC=42°,OD平分∠AOC.求∠AOD的度数. 如图,∠AOB=42゜,∠BOC=86゜,OD为∠AOC的平分线,求∠BOD的度数.
如图,∠AOB=42゜,∠BOC=86゜,OD为∠AOC的平分线,求∠BOD的度数.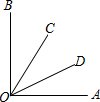 如图,∠AOB=90°,∠BOC=42°,OD平分∠AOC.求∠AOD的度数.
如图,∠AOB=90°,∠BOC=42°,OD平分∠AOC.求∠AOD的度数.