题目内容
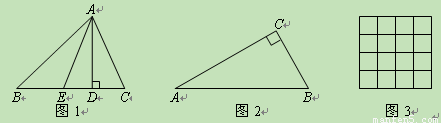
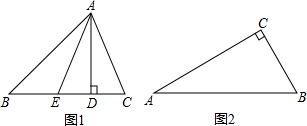
如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=| DE | BE |
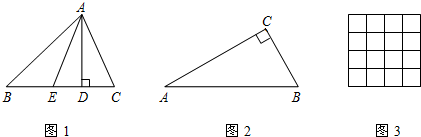
(1)如图2,在△ABC中,∠C=90°,∠A=30°,求λA、λC;
(2)在每个小正方形边长均为1的4×4的方格纸上,画一个△ABC,使其顶点在格点(格点即每个小正方形的顶点)上,且λA=2,面积也为2;
(3)判断下列三个命题的真假(真命题打“√”,假命题打“×”):
①若△ABC中λA<1,则△ABC为锐角三角形;
②若△ABC中λA=1,则△ABC为直角三角形;
③若△ABC中λA>1,则△ABC为钝角三角形.
分析:(1)根据直角三角形斜边中线、高的特点进行转换即可得出答案,
(2)根据题目要求即可画出图象,
(3)根据真假命题的定义即可得出答案.
(2)根据题目要求即可画出图象,
(3)根据真假命题的定义即可得出答案.
解答: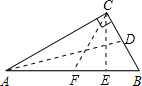 解:(1)如图,作BC边上的中线AD,又AC⊥DC,
解:(1)如图,作BC边上的中线AD,又AC⊥DC,
∴λA=
=1,
过点C分别作AB边上的高CE和中线CF,
∵∠ACB=90°,
∴AF=CF,
∴∠ACF=∠CAF=30°,
∴∠CFE=60°,
∴λC=
=
=cos60°=
;
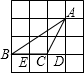
(2)如图:
(3)①×,②√,③√.
 解:(1)如图,作BC边上的中线AD,又AC⊥DC,
解:(1)如图,作BC边上的中线AD,又AC⊥DC,∴λA=
| CD |
| BD |
过点C分别作AB边上的高CE和中线CF,
∵∠ACB=90°,
∴AF=CF,
∴∠ACF=∠CAF=30°,
∴∠CFE=60°,
∴λC=
| EF |
| AF |
| EF |
| CF |
| 1 |
| 2 |

(2)如图:
(3)①×,②√,③√.
点评:本题主要考查了直角三角形斜边中线、高的性质以及特殊角的三角函数值,同时考查了画图,真假命题的判断,比较复杂,难度较大.

练习册系列答案
相关题目
 如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=
如图1,AD和AE分别是△ABC的BC边上的高和中线,点D是垂足,点E是BC的中点,规定:λA=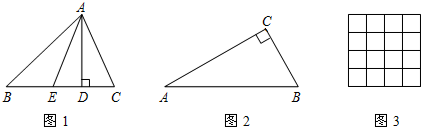
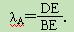 .特别地,当点D、E重合时,规定:λA
.特别地,当点D、E重合时,规定:λA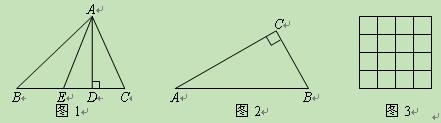
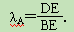 .特别地,当点D、E重合时,规定:λA
.特别地,当点D、E重合时,规定:λA