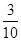题目内容
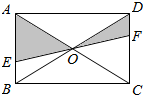 如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的( )
如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,那么阴影部分的面积是矩形ABCD的面积的( )A、
| ||
B、
| ||
C、
| ||
D、
|
分析:本题主要根据矩形的性质,得△EBO≌△FDO,再由△AOB与△OBC同底等高,△AOB与△ABC同底且△AOB的高是△ABC高的
得出结论.
| 1 |
| 2 |
解答:解:∵四边形为矩形,
∴OB=OD=OA=OC,
在△EBO与△FDO中,
∵
,
∴△EBO≌△FDO(ASA),
∴阴影部分的面积=S△AEO+S△EBO=S△AOB,
∵△AOB与△ABC同底且△AOB的高是△ABC高的
,
∴S△AOB=S△OBC=
S矩形ABCD.
故选:B.
∴OB=OD=OA=OC,
在△EBO与△FDO中,
∵
|
∴△EBO≌△FDO(ASA),
∴阴影部分的面积=S△AEO+S△EBO=S△AOB,
∵△AOB与△ABC同底且△AOB的高是△ABC高的
| 1 |
| 2 |
∴S△AOB=S△OBC=
| 1 |
| 4 |
故选:B.
点评:本题考查矩形的性质,矩形具有平行四边形的性质,又具有自己的特性,要注意运用矩形具备而一般平行四边形不具备的性质.

练习册系列答案
相关题目
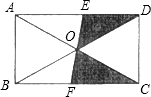 如图,EF过矩形ABCD对角线的交点O,且分别交AD、BC于点E、F已知AB=3,BC=4,则图中阴影部分的面积是( )
如图,EF过矩形ABCD对角线的交点O,且分别交AD、BC于点E、F已知AB=3,BC=4,则图中阴影部分的面积是( ) (2013•历城区一模)如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,矩形ABCD内的一个动点P落在阴影部分的概率是( )
(2013•历城区一模)如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,矩形ABCD内的一个动点P落在阴影部分的概率是( )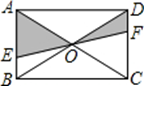
 B.
B.  C.
C. 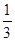 D.
D.