题目内容
如图,点A,B分别在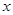 轴,
轴, 轴上,点D在第一象限内,DC⊥
轴上,点D在第一象限内,DC⊥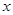 轴于点C,AO=CD=2,AB=DA=
轴于点C,AO=CD=2,AB=DA= ,反比例函数
,反比例函数 的图象过CD的中点E。
的图象过CD的中点E。
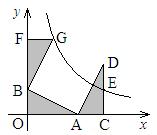
(1)求证:△AOB≌△DCA;
(2)求 的值;
的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在 轴上,试判断点G是否在反比例函数的图象上,并说明理由。(
轴上,试判断点G是否在反比例函数的图象上,并说明理由。(
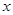 轴,
轴, 轴上,点D在第一象限内,DC⊥
轴上,点D在第一象限内,DC⊥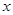 轴于点C,AO=CD=2,AB=DA=
轴于点C,AO=CD=2,AB=DA= ,反比例函数
,反比例函数 的图象过CD的中点E。
的图象过CD的中点E。
(1)求证:△AOB≌△DCA;
(2)求
 的值;
的值;(3)△BFG和△DCA关于某点成中心对称,其中点F在
 轴上,试判断点G是否在反比例函数的图象上,并说明理由。(
轴上,试判断点G是否在反比例函数的图象上,并说明理由。((1)证明见解析
(2)K=3
(3)点G在反比例函数图象上
(2)K=3
(3)点G在反比例函数图象上
试题分析:(1)利用HL可证△AOB≌△DCA
由勾股定理可求出AC的长,从而得到OC的长,可得E坐标,代入即得
(3)由△BFG和△DCA关于某点成中心对称可知BF=DC=2,FG=AC=1,从而可得点G坐标,代入判断即可
试题解析:(1)∵点A,B分别在X,Y轴上,DC⊥X轴于点C
∴∠AOB=∠DCA=90°
∵AO=CD=2,AB=DA=

∴△AOB≌△DCA
(2)∵∠DCA=90°,DA=
 ,CD=2
,CD=2∴AC=
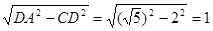
∴OC=OA+AC=2+1=3
∵E是CD的中点
∴E(3,1)
∵反比例函数
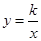 的图象过点E
的图象过点E∴K=3
(3)∵△BFG和△DCA关于某点成中心对称
∴BF=DC=2,FG=AC=1
∵点F在Y轴上
∴OF=OB+BF=1+2=3
∴G(1,3)
把X=1代入
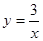 中得Y=3
中得Y=3∴点G在反比例函数图象上

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
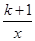 经过点(-1,2),那么k的值等于 .
经过点(-1,2),那么k的值等于 . (k>0)的图象上,则y1 y2(填“>”“<”或“=”)
(k>0)的图象上,则y1 y2(填“>”“<”或“=”) (k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是( )
(k≠0)交于A、B两点,过点B作BC⊥x轴于点C,作BD⊥y轴于点D.在x轴上分别取点E、F,使点A、E、F在同一条直线上,且AE=AF.设图中矩形ODBC的面积为S1,△EOF的面积为S2,则S1、S2的数量关系是( )
 上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD=
上两点,AC⊥y轴于C,BD⊥x轴于D,AC=BD= OC,S四边形ABDC=9,则k= .
OC,S四边形ABDC=9,则k= .