题目内容
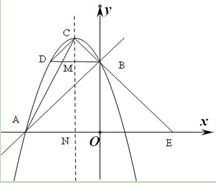
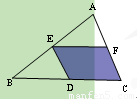
(2011内蒙古赤峰,24,12分)如图,直线y=x+3与坐标轴分别交于A、B两点,抛物线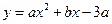 经过点A、B,顶点为C,连结CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称。
经过点A、B,顶点为C,连结CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称。(1)求抛物线的解析式及顶点C的坐标;
(2)求证:四边形ABCD是直角梯形。
解:(1)∵直线y=x+3与坐标轴分别交于A、B两点。
当y=0时,x=-3,∴点A的坐标为(-3,0)
当x =0时,y= 3,∴点B的坐标为(0,3)
把A(-3,0)、B(0,3)代入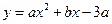 中得:
中得:
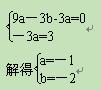
∴抛物线的解析式为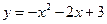
∵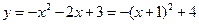
∴C点的坐标为(-1,4)。
(2)证明:
方法(一)∵A(-3,0)、B(0,3)、C(-1,4);
∴OA=OB=3,AN=2,CN=4,CM=MB=1.
在Rt△AOB中,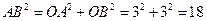 ;
;
在Rt△ANC中, ;
;
在Rt△CMB中,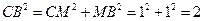 ;
;
∴ ,∴∠ABC=90°
,∴∠ABC=90°
∵点D、B关于对称轴CN对称,∠BCM=45°;
∴∠DCM=45°,则∠DCB=90°;
∴DC∥AB ;
∵AD≠CB ;
∴四边形ABCD是直角梯形
方法(二):设直线BC的解析式为y=mx+3;
把C(-1,4)代入,得m=-1;
∴直线BC的解析式为y=-x+3;
当y=0时,x=3,则E点的坐标为(3,0),即OE="3" ;
∵A(-3,0)、B(0,3);
∴OA="OB=OE=3" 。
∵∠BOA="∠BOE" =90°
∴∠BAO="∠ABO=∠OEB" =∠OBE=45°;
∴∠ABE=90°;
∴∠ABC=90°;
∵点D、B关于对称轴CN对称,∠BCM=45°;
∴∠DCM=45°,则∠DCB=90°;
∴DC∥AB ;
∵AD≠CB ;
∴四边形ABCD是直角梯形解析:
略
当y=0时,x=-3,∴点A的坐标为(-3,0)
当x =0时,y= 3,∴点B的坐标为(0,3)
把A(-3,0)、B(0,3)代入
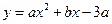 中得:
中得: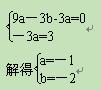
∴抛物线的解析式为
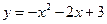
∵
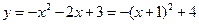
∴C点的坐标为(-1,4)。
(2)证明:
方法(一)∵A(-3,0)、B(0,3)、C(-1,4);
∴OA=OB=3,AN=2,CN=4,CM=MB=1.
在Rt△AOB中,
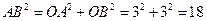 ;
;在Rt△ANC中,
 ;
;在Rt△CMB中,
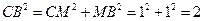 ;
;∴
 ,∴∠ABC=90°
,∴∠ABC=90°∵点D、B关于对称轴CN对称,∠BCM=45°;
∴∠DCM=45°,则∠DCB=90°;
∴DC∥AB ;
∵AD≠CB ;
∴四边形ABCD是直角梯形
方法(二):设直线BC的解析式为y=mx+3;
把C(-1,4)代入,得m=-1;
∴直线BC的解析式为y=-x+3;
当y=0时,x=3,则E点的坐标为(3,0),即OE="3" ;
∵A(-3,0)、B(0,3);
∴OA="OB=OE=3" 。
∵∠BOA="∠BOE" =90°
∴∠BAO="∠ABO=∠OEB" =∠OBE=45°;
∴∠ABE=90°;
∴∠ABC=90°;
∵点D、B关于对称轴CN对称,∠BCM=45°;
∴∠DCM=45°,则∠DCB=90°;
∴DC∥AB ;
∵AD≠CB ;
∴四边形ABCD是直角梯形解析:
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
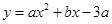 经过点A、B,顶点为C,连结CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称。
经过点A、B,顶点为C,连结CB并延长交x轴于点E,点D与点B关于抛物线的对称轴MN对称。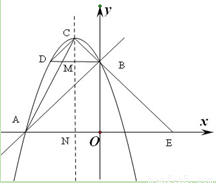
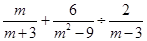 的结果是____________。
的结果是____________。