题目内容
 如图,一个边长为3、4、5厘米的直角三角形的一个顶点与正方形的顶点B重合,另两个顶点分别在正方形的两条边AD、DC上,那么这个正方形的面积是________厘米2.
如图,一个边长为3、4、5厘米的直角三角形的一个顶点与正方形的顶点B重合,另两个顶点分别在正方形的两条边AD、DC上,那么这个正方形的面积是________厘米2.

分析:设BC=a,根据勾股定理可以求得CE的长,易证△BCE∽△EDF得DE=
 a,再根据DE+EC=DC即可求得a的值,即可求得正方形的面积,即可解题.
a,再根据DE+EC=DC即可求得a的值,即可求得正方形的面积,即可解题.解答:设BC=a,则CE=
 ,
,∵∠BEC+∠EBC=90°,∠BEC+∠DEF=90°,
∴∠DEF=∠CBE,又∵∠BCE=∠EDF=90°,
∴△BCE∽△EDF,
得 DE=
 a,又DE+EC=DC,即
a,又DE+EC=DC,即 a+
a+ =a,
=a,解得a2=
 .
.故答案为:
 .
.点评:本题考查了相似三角形的证明和相似三角形对应边比值相等的性质,考查了勾股定理在直角三角形中的运用,本题中根据DE+EC=DC求a的值是解题的关键.

练习册系列答案
相关题目
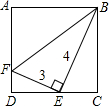 如图,一个边长为3、4、5厘米的直角三角形的一个顶点与正方形的顶点B重合,另两个顶点分别在正方形的两条边AD、DC上,那么这个正方形的面积是
如图,一个边长为3、4、5厘米的直角三角形的一个顶点与正方形的顶点B重合,另两个顶点分别在正方形的两条边AD、DC上,那么这个正方形的面积是 如图是一个边长为a的正方形,用代数式表示图中的阴影部分的面积,并求当a=2cm时,阴影部分的面积是多少?(π取3.14,结果保留一位小数)
如图是一个边长为a的正方形,用代数式表示图中的阴影部分的面积,并求当a=2cm时,阴影部分的面积是多少?(π取3.14,结果保留一位小数) 如图,一个边长为a的小正方形与两个长、宽分别为a,b的小矩形拼成一个大矩形,则由整个图形的面积关系可以得到一个有关多项式因式分解的等式,这个等式是
如图,一个边长为a的小正方形与两个长、宽分别为a,b的小矩形拼成一个大矩形,则由整个图形的面积关系可以得到一个有关多项式因式分解的等式,这个等式是 如图把一个边长为4厘米的正方形剪成四个相同的四个直角三角形,把这四个三角形按要求拼图
如图把一个边长为4厘米的正方形剪成四个相同的四个直角三角形,把这四个三角形按要求拼图 n次取走后,还剩
n次取走后,还剩