题目内容
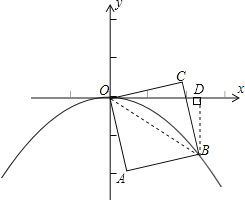
【题目】如图，OABC是边长为1的正方形，OC与x轴正半轴的夹角为15°，点B在抛物线y=ax2的图象上，则a的值为（ )
A. 
B. 
C. 
D. 
【答案】B
【解析】
连接OB，根据正方形的对角线平分一组对角线可得∠BOC=45°，过点B作BD⊥x轴于D，然后求出∠BOD=30°，根据直角三角形30°角所对的直角边等于斜边的一半可得
，再利用勾股定理列式求出OD，从而得到点B的坐标，再把点B的坐标代入抛物线解析式求解即可．
如图，连接OB，
∵四边形OABC是边长为1的正方形，
∴
过点B作BD⊥x轴于D，
∵OC与x轴正半轴的夹角为
∴
∴
∴点B的坐标为
∵点B在抛物线y=ax2(a<0)的图象上，
∴
解得a=
故选：B.
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
