题目内容
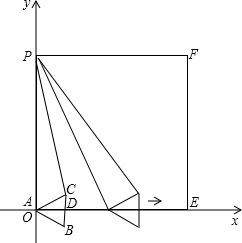
 如图,边长为2
如图,边长为2| 3 |
(1)求⊙0的半径;
(2)设AD为x,AP为y,求出y与x的函数关系式及自变量x的取值范围.
分析:(1)过O作OE⊥AB于E,连接OA,根据等边三角形的性质和垂径定理可以E是AB的中点∠EAO=30°这样解直角三角形就可以求出半径了;
(2)连接CD,利用圆内接四边形的性质可以得到∠ADC=∠ACP=120°,还有一个公共角,可以证明△ADC∽△ACP,然后利用相似三角形的性质就可以求出函数的关系式.
(2)连接CD,利用圆内接四边形的性质可以得到∠ADC=∠ACP=120°,还有一个公共角,可以证明△ADC∽△ACP,然后利用相似三角形的性质就可以求出函数的关系式.
解答:解: 解:(1)过O作OE⊥AB于E,连接OA.
解:(1)过O作OE⊥AB于E,连接OA.
在Rt△AEO中,∠EAO=30°
AE=
∴
=cos30°,
∴OA=2
(2)连接CD,则∠ABC+∠ADC=180°
又∠ACB+∠ACP=180°,∠ABC=∠ACB=60°
∴∠ADC=∠ACP=120°
又∵∠CAD=∠PAC
∴△ADC∽△ACP
∴
∴AC2=AD•AP
∴y=
=
(0<x<2
).
 解:(1)过O作OE⊥AB于E,连接OA.
解:(1)过O作OE⊥AB于E,连接OA.在Rt△AEO中,∠EAO=30°
AE=
| AB |
| 2 |
∴
| AE |
| OA |
∴OA=2
(2)连接CD,则∠ABC+∠ADC=180°
又∠ACB+∠ACP=180°,∠ABC=∠ACB=60°
∴∠ADC=∠ACP=120°
又∵∠CAD=∠PAC
∴△ADC∽△ACP
∴
| AD |
| AC |
| AC |
| AP |
∴AC2=AD•AP
∴y=
(2
| ||
| x |
| 12 |
| x |
| 3 |
点评:此题综合性比较强,把一元二次方程,等边三角形,相似三角形,求函数关系式等知识,正确作出辅助线是关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目

 如图,已知△ABC是边长为2
如图,已知△ABC是边长为2