题目内容
在上劳技课时,张老师拿出一张边长为2| 3 |
(1)写出点M的坐标;
(2)求出m与n的函数关系式,并求自变量n的取值范围约在哪两个数之间(精确到0.1);
(3)若记这四个圆的面积总和为S,试问S有最小值吗?若有,求出这个最小值,并写出相应的m值.
分析:(1)连接AM并延长交BC于N,根据等边三角形的性质求出BN,根据勾股定理求出AN,求出ON即可;
(2)连接DO3,求出AO3=2DO3=2n,根据AN的长度得到3=1+m+m+n+2n求出即可;
(3)根据圆的面积公式得到S=πm2+3πn2,代入求出即可.
(2)连接DO3,求出AO3=2DO3=2n,根据AN的长度得到3=1+m+m+n+2n求出即可;
(3)根据圆的面积公式得到S=πm2+3πn2,代入求出即可.
解答: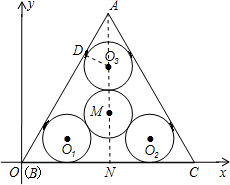 解:(1)连接AM并延长交BC于N,
解:(1)连接AM并延长交BC于N,
∵M是等边△ABC的中心,
∴AM=2NM,AN⊥BC,CN=BN,∠BAN=
∠BAC=30°,
由勾股定理得:AN=
=3,
∴MN=1,
∴M(
,1),
答:点M的坐标是(
,1).
(2)连接DO3,
∵∠BAN=30°,∠O3DA=90°,
∴AO3=2DO3=2n,
∴3=1+m+m+n+2n,
∴m=-3n+2,(0.3<n<0.6);
答:m与n的函数关系式是m=-3n+2,并求自变量n的取值范围约在0.3-0.6之间.
(3)S=πm2+3πn2=π(-3n+2)2+3πn2=π(12 n2-12n+4)=12π(n-0.5)2+π,
当n=0.5,即m=0.5时,S有最小值,最小值为S=π.
答:S有最小值,这个最小值是π,m值是0.5.
 解:(1)连接AM并延长交BC于N,
解:(1)连接AM并延长交BC于N,∵M是等边△ABC的中心,
∴AM=2NM,AN⊥BC,CN=BN,∠BAN=
| 1 |
| 2 |
由勾股定理得:AN=
(2
|
∴MN=1,
∴M(
| 3 |
答:点M的坐标是(
| 3 |
(2)连接DO3,
∵∠BAN=30°,∠O3DA=90°,
∴AO3=2DO3=2n,
∴3=1+m+m+n+2n,
∴m=-3n+2,(0.3<n<0.6);
答:m与n的函数关系式是m=-3n+2,并求自变量n的取值范围约在0.3-0.6之间.
(3)S=πm2+3πn2=π(-3n+2)2+3πn2=π(12 n2-12n+4)=12π(n-0.5)2+π,
当n=0.5,即m=0.5时,S有最小值,最小值为S=π.
答:S有最小值,这个最小值是π,m值是0.5.
点评:本题主要考查对等边三角形的性质,二次函数的最值,相切两圆的性质,勾股定理,含30度角的直角三角形性质,坐标与图形性质等知识点的连接和掌握,能综合运用这些性质进行推理和计算是解此题的关键.

练习册系列答案
 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目

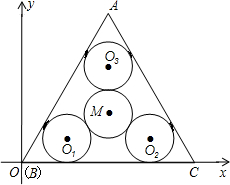
 的等边△ABC纸片,现要在这块纸片上裁剪出四个圆,若记这块△ABC纸片的中心为M,半径为m,在△ABC内部画一个⊙M后,再作三个半径都为n的等圆⊙O1、⊙O2、⊙O3,使它们分别与△ABC的两边相切,与⊙M外切,建立直角坐标系如图所示.
的等边△ABC纸片,现要在这块纸片上裁剪出四个圆,若记这块△ABC纸片的中心为M,半径为m,在△ABC内部画一个⊙M后,再作三个半径都为n的等圆⊙O1、⊙O2、⊙O3,使它们分别与△ABC的两边相切,与⊙M外切,建立直角坐标系如图所示.
 的等边△ABC纸片,现要在这块纸片上裁剪出四个圆,若记这块△ABC纸片的中心为M,半径为m,在△ABC内部画一个⊙M后,再作三个半径都为n的等圆⊙O1、⊙O2、⊙O3,使它们分别与△ABC的两边相切,与⊙M外切,建立直角坐标系如图所示.
的等边△ABC纸片,现要在这块纸片上裁剪出四个圆,若记这块△ABC纸片的中心为M,半径为m,在△ABC内部画一个⊙M后,再作三个半径都为n的等圆⊙O1、⊙O2、⊙O3,使它们分别与△ABC的两边相切,与⊙M外切,建立直角坐标系如图所示.