Question

有三个完全相同的小球，上面分别标有数字1，-2，-3，将其放入一个不透明的盒子中摇匀，再从中随机摸球两次（第一次摸出球后放回摇匀），设第一次摸到的球上所标的数字为m，第二次摸到的球上所标的数字为n，依次以m、n作为点M的横、纵坐标．
（1）用树状图（或列表法）表示出点M（m，n）的坐标所有可能的结果；
（2）求点M（m，n）在第三象限的概率．

Answer 1

分析：通过树状图或列表，列举出所有情况，再计算概率即可．

解答：解：（1）组成的点M（m，n）的坐标的所有可能性为：

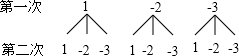
得到的各点为（1，1）；（1，-2）；（1，-3）；（-2，1）；（-2，-2）；（-2，-3）；（-3，1）；（-3，-2）；（-3，-3）．
（2）落在第三象限的点有（-2，-2），（-2，-3），（-3，-2），（-3，-3），因此点M落在第三象限的概率为

4

9

．（5分）

点评：用到的知识点为：概率=所求情况数与总情况数之比．第三象限点的符号为（-，-）．