Question

有A，B两个黑布袋，A布袋中有两个完全相同的小球，分别标有数字1和2．B布袋中有三个完全相同的小球，分别标有数字-1，-2和2．小明从A布袋中随机取出一个小球，记录其标有的数字为x，再从B布袋中随机取出一个小球，记录其标有的数字为y，这样就确定点Q的一个坐标为（x，y）．
（1）用列表或画树状图的方法写出点Q的所有可能坐标；
（2）求点Q落在直线y=x-3上的概率．

Answer 1

分析：（1）根据题意画树状图，然后根据树状图求得所有等可能的结果，即可求得点Q的所有可能坐标；
（2）根据（1）中的树状图，求得点Q落在直线y=x-3上的情况，根据概率公式求解即可求得答案．

解答：解：（1）树状图如下：

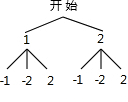
∴Q点的所有可能是Q（1，-1）；Q（1，2）；Q（1，-2）；Q（2，-1）；Q（2，2）；Q（2，-2）．

（2）∵只有Q（1，-2），Q（2，-1）在直线y=x-3上，
∴点Q落在直线y=x-3上的概率为：

2

6

=

1

3

．

点评：此题考查了列表法或树状图法求概率．注意列表法与树状图法可以不重不漏的表示出所有等可能的结果．用到的知识点为：概率=所求情况数与总情况数之比．