题目内容
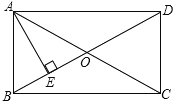
【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,AE⊥BD于E,若BE:ED=1:3,AD=6. (1)求∠BAE的度数;(2)求AE的长.
【答案】(1)、30°;(2)、3.
【解析】
试题分析:(1)、根据矩形的性质可得:OB=OD,OA=OC,AC=BD,OA=OB,根据BE:ED=1:3,得出BE:OB=1:2,从而说明BE=0E,得出△ABE和△AEO全等,从而得出△AOB为等边三角形,根据等边三角形的性质得出∠BAE的度数;(2)、根据等边三角形的性质得出∠ADE的度数,然后根据直角三角形的性质求出AE的长度.
试题解析:(1)、∵四边形ABCD是矩形,∴OB=OD,OA=OC,AC=BD,∴OA=OB
∵BE:ED=1:3,∴BE:OB=1:2,∴BE=OE ∵AE⊥BD∴![]()
在△AEB和△AEO中 ∴△AEB≌△AEO ∴AB=AO,∴OA=AB=OB,
∴△AEB≌△AEO ∴AB=AO,∴OA=AB=OB,
即△OAB是等边三角形,∴∠BAE=30°
(2)、∵△OAB是等边三角形,∴∠ABD=60° ∴∠ADE=90°﹣∠ABD=30°
∵AE⊥BD,AD=6,∴AE=![]() AD=3.
AD=3.

练习册系列答案
相关题目