��Ŀ����
 ����ƽ��ֱ������ϵ�е���������P1��x1��y1����P2��x2��y2�������ǰ�|x1-x2|+|y1-y2|����P1��P2������ֱ�Ǿ��룬����d��P1��P2����
����ƽ��ֱ������ϵ�е���������P1��x1��y1����P2��x2��y2�������ǰ�|x1-x2|+|y1-y2|����P1��P2������ֱ�Ǿ��룬����d��P1��P2����
��1����֪OΪ����ԭ�㣬����P��x��y������d��O��P��=1����д��x��y֮������Ĺ�ϵʽ������������ֱ������ϵ�л������з��������ĵ�P����ɵ�ͼ�Σ�
��2����P0��x0��y0����һ���㣬Q��x��y����ֱ��y=ax+b�ϵĶ��㣬���ǰ�d��P0��Q������Сֵ����P0��ֱ��y=ax+b��ֱ�Ǿ��룮�����M��2��1����ֱ��y=x+2��ֱ�Ǿ��룮
 �⣺��1�������⣬��|x|+|y|=1��
�⣺��1�������⣬��|x|+|y|=1����d��O��P��=1��O��0��0����P��x��y��
��d��0��P��=|x|+|y|
��|x|+|y|=1
��x��0��y��0
��x+y=1
y=1-x
��x��0��y��0
��-x-y=1
y=-x-1
��x��0��y��0
��x-y=1
y=x-1
��x��0��y��0
��-x+y=1
y=1+x
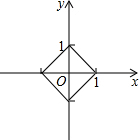
���ĸ�������ϵʽ��ʾ�������ϣ����з��������ĵ�P��ɵ�ͼ����ͼ��ʾ��
��2����d��M��Q��=|x-2|+|y-1|=|x-2|+|x+2-1|=|x-2|+|x+1|��
�֡�x��ȡһ��ʵ����|x-2|+|x+1|��ʾ������ʵ��x����Ӧ�ĵ㵽��2��-1����Ӧ�ĵ�ľ���֮�ͣ�����СֵΪ3��
���M��2��1����ֱ��y=x+2��ֱ�Ǿ���Ϊ3��
��������1�������µ��������֪|x|+|y|=1���ݴ˿��Ի������������ͼ�Σ�
��2�������µ��������֪d��M��Q��=|x-2|+|y-1|=|x-2|+|x+2-1|=|x-2|+|x+1|��Ȼ���ɾ���ֵ������Ĺ�ϵ��֪��|x-2|+|x+1|��ʾ������ʵ��x����Ӧ�ĵ㵽��2��-1����Ӧ�ĵ�ľ���֮�ͣ�����СֵΪ3��
���������⿼����һ�κ����ۺ��⣮��ȷ�����¶������㷨���ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
 ��2012•����������ƽ��ֱ������ϵ�е���������P1��x1��y1����P2��x2��y2�������ǰ�|x1-x2|+|y1-y2|����P1��P2������ֱ�Ǿ��룬����d��P1��P2����
��2012•����������ƽ��ֱ������ϵ�е���������P1��x1��y1����P2��x2��y2�������ǰ�|x1-x2|+|y1-y2|����P1��P2������ֱ�Ǿ��룬����d��P1��P2����