题目内容
【题目】如图1，已知抛物线y＝ax2＋bx （a≠0）经过A（3，0）、B（4，4）两点．
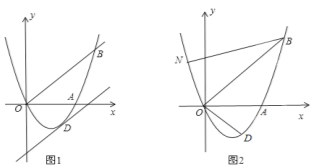
（1）求抛物线的解析式；
（2）将直线OB向下平移m个单位长度后，得到的直线与抛物线只有一个公共点D，求m的值及点D的坐标；
（3）如图2，若异于点A的点N在抛物线上，且∠NBO＝∠ABO，求点N的坐标；
【答案】（1）
；（2）
点的坐标为
；（3）
【解析】
试题分析：（1）利用待定系数法求二次函数解析式进而得出答案即可；
根据已知条件可求出的解析式为
，则向下平移
个单位长度后的解析式为：
由于抛物线与直线只有一个公共点，则联立解析式后得到的一元二次方程，其根的判别式等于0，由此可求出的值和点坐标；
设点
，又点
在抛物线上，代入抛物线的解析式即可求出
的值，进而得到的坐标．
试题解析：（1）抛物线
经过
，将
与两点坐标代入得：
，解得：
，抛物线的解析式是
设直线
的解析式为
，由点
，得：
，解得：
．直线的解析式为，直线向下平移个单位长度后的解析式：
在抛物线上，可设
点D在直线
上，
，即
，
抛物线与直线只有一个公共点，
解得：
此时
点的坐标为
直线的解析式为，且A（3，0），
点A关于直线的对称点
的坐标是（0，3），根据轴对称性质和三线合一性质得出
，设直线
的解析式为
，过点（4，4），
解得：
，直线的解析式是
，
和
重合，即点N在直线上，设点，又点在抛物线上，
解得：
（不合题意，舍），
练习册系列答案
小学期末标准试卷系列答案
相关题目