题目内容
如图,是一个直径为650㎜的圆柱形输油管的横截面,若油面宽AB=600㎜,求油面的最大深度.
【答案】分析:先过点O作OD⊥AB于点D,交 于点F,连接OA,有垂径定理可求出AD的长,再根据勾股定理求出OD的长,进而可得出DF的长.
于点F,连接OA,有垂径定理可求出AD的长,再根据勾股定理求出OD的长,进而可得出DF的长.
解答: 解:过点O作OD⊥AB于点D,交
解:过点O作OD⊥AB于点D,交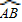 于点F,连接OA,
于点F,连接OA,
∵AB=600mm,
∴AD=300mm,
∵底面直径为650mm,
∴OA= ×650=325mm,
×650=325mm,
∴OD= =
=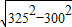 =125mm,
=125mm,
∴DF=OF-OD= ×650-125=200mm.
×650-125=200mm.
答:油面的最大深度为200mm.
点评:此题主要考查了垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
 于点F,连接OA,有垂径定理可求出AD的长,再根据勾股定理求出OD的长,进而可得出DF的长.
于点F,连接OA,有垂径定理可求出AD的长,再根据勾股定理求出OD的长,进而可得出DF的长.解答:
 解:过点O作OD⊥AB于点D,交
解:过点O作OD⊥AB于点D,交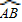 于点F,连接OA,
于点F,连接OA,∵AB=600mm,
∴AD=300mm,
∵底面直径为650mm,
∴OA=
 ×650=325mm,
×650=325mm,∴OD=
 =
=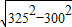 =125mm,
=125mm,∴DF=OF-OD=
 ×650-125=200mm.
×650-125=200mm.答:油面的最大深度为200mm.
点评:此题主要考查了垂径定理的应用及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,是一个直径为650㎜的圆柱形输油管的横截面,若油面宽AB=600㎜,求油面的最大深度.
如图,是一个直径为650㎜的圆柱形输油管的横截面,若油面宽AB=600㎜,求油面的最大深度. 如图,是一个直径为100㎜的圆柱形输油管的横截面,若油面宽AB=80㎜,求油面的最大深度.
如图,是一个直径为100㎜的圆柱形输油管的横截面,若油面宽AB=80㎜,求油面的最大深度. 如图,是一个直径为100㎜的圆柱形输油管的横截面,若油面宽AB=80㎜,求油面的最大深度.
如图,是一个直径为100㎜的圆柱形输油管的横截面,若油面宽AB=80㎜,求油面的最大深度.