题目内容
一条弦把圆分成4:5的两部分,那么这条弦所对圆周角的度数是 度.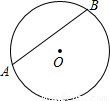
【答案】分析:先根据弦把圆分成4:5的两部分求出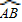 与
与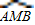 的度数,进而可得出∠AOB的度数,由圆周角定理可求出∠AMB的度数.
的度数,进而可得出∠AOB的度数,由圆周角定理可求出∠AMB的度数.
解答: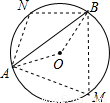 解:∵弦AB把⊙O分成4:5的两部分,
解:∵弦AB把⊙O分成4:5的两部分,
∴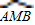 =360°×
=360°× =200°,
=200°,
∴∠AOB=200°,
∴∠AMB= ∠AOB=
∠AOB= ×200°=100°,∠ANB=180°-∠AMB=180°-100°=80°.
×200°=100°,∠ANB=180°-∠AMB=180°-100°=80°.
故答案为:80或100.
点评:本题考查的是圆心角、弧、弦的关系及圆周角定理,根据题意作出辅助线,构造出圆周角及圆心角是解答此题的关键.
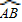 与
与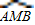 的度数,进而可得出∠AOB的度数,由圆周角定理可求出∠AMB的度数.
的度数,进而可得出∠AOB的度数,由圆周角定理可求出∠AMB的度数.解答:
 解:∵弦AB把⊙O分成4:5的两部分,
解:∵弦AB把⊙O分成4:5的两部分,∴
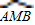 =360°×
=360°× =200°,
=200°,∴∠AOB=200°,
∴∠AMB=
 ∠AOB=
∠AOB= ×200°=100°,∠ANB=180°-∠AMB=180°-100°=80°.
×200°=100°,∠ANB=180°-∠AMB=180°-100°=80°.故答案为:80或100.
点评:本题考查的是圆心角、弧、弦的关系及圆周角定理,根据题意作出辅助线,构造出圆周角及圆心角是解答此题的关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
 一条弦把圆分成4:5的两部分,那么这条弦所对圆周角的度数是
一条弦把圆分成4:5的两部分,那么这条弦所对圆周角的度数是